Halting Problem

ปัญหา Halting Problem เนี่ย เป็นปัญหาสุดคลาสสิกอันนึงสำหรับคนที่เรียนคอมพิวเตอร์ โจทย์มีอยู่ว่า

เราจะสร้างโปรแกรม (หรือคำสั่ง) ชื่อว่า H ที่รับ input 2 ตัว คือ

1. X = โปรแกรม (คือ source code หรือ object code หรือ อะไรก็ได้)
2. Y = input (ทั้งหมด) ของโปรแกรม X

และมี output เป็น

1. "หยุด" ถ้า X(Y) หยุดการทำงานในเวลาจำกัด
2. "ไม่หยุด" ถ้า X(Y) ไม่หยุดการทำงาน (ก็คือ ติด loop หนะ)

โดยที่ H(X, Y) ทำงานเสร็จในเวลาจำกัด (นับเป็นจำนวนคำสั่งก็ได้) ได้รึเปล่า?

H(X, Y) ทำงานเสร็จในเวลาจำกัด แปลว่า H(H, (X, Y)) ให้คำตอบเป็น "หยุด" เสมอน่ะนะ

คำตอบของปัญหานี้ ก็มีคนตอบได้มานานแล้วหละ แต่วิธีการหาคำตอบเนี่ย น่าสนใจ ... เค้าใช้วิธีพิสูจน์แบบขัดแย้ง แบบนี้...

สมมติว่า H(X, Y) มีอยู่จริง เราจะสร้างโปรแกรม L(X) แบบนี้ได้

L(X)

• If H(X, X) = "หยุด", then loop forever.
• Else (if H(X, X) = "ไม่หยุด"), do nothing.

แปลว่า ถ้า H(X, X) ให้คำตอบเป็น "หยุด" H(L, X) จะเป็น "ไม่หยุด" แต่ถ้า H(X, X) ให้คำตอบเป็น "ไม่หยุด" H(L, X) จะเป็น "หยุด"

คราวนี้ เราก็ลองคิดดูว่า H(L, L) มันจะเป็นอะไร ...

ถ้า H(L, L) = "หยุด"

1. ตามนิยามของ H: L(L) ต้องหยุด
2. ตามนิยามของ L: แปลว่ามันไปตกที่ "Else, ..." ดังนั้น H(L, L) = "ไม่หยุด"

ถ้า H(L, L) = "ไม่หยุด"

1. ตามนิยามของ H: L(L) ต้องไม่หยุด
2. ตามนิยามของ L: แปลว่ามันไปตกที่ "If ..., then ..." ดังนั้น H(L, L) = "หยุด"

จะเห็นว่า ไม่ว่าจะสมมติให้ H(L, L) เป็นอะไร มันก็จะเกิดความขัดแย้งเสมอ แสดงว่า จริง ๆ แล้วเราไม่สามารถสร้าง H ได้นั่นเอง

ความพยายามสร้าง H(X, Y) ที่ใกล้เคียงที่สุด ก็คือ

1. H(X, Y) ตอบว่า "หยุด" ในเวลาจำกัด ถ้า X(Y) หยุดการทำงานในเวลาจำกัด
2. H(X, Y) ไม่สามารถตอบอะไรได้ และไม่หยุดการทำงาน ถ้า X(Y) ไม่หยุดการทำงาน

ซึ่ง H(X, Y) แบบนี้ ก็ไม่ต่างจากการปล่อยให้ X(Y) ทำงานเฉย ๆ

โยงกลับไปที่ภาษาอันดับหนึ่งนิดนึง เคยพูดไว้ในตอนท้ายเรื่อง ตรรกศาสตร์: Unification แล้วว่า

"จะว่าไป มันก็เทียบได้กับ halting problem น่ะแหละ (เทียบได้จริง ๆ นะ เหมือนกัันเด๊ะเลย)"

ก็เลยเอามาเทียบกันให้ดูอีกที ว่าทำไมมันเหมือนกัน ... อันนี้คือ ความเป็นจริงเกี่ยวกับการพิสูจน์ว่า ประพจน์เป็นจริงรึเปล่า เมื่อมีกฎต่าง ๆ ให้

"ถ้าประพจน์ที่ต้องการพิสูจน์เป็นจริง เมื่อได้ประพจน์ว่าง (จาก resolution) เราก็จะรู้ แต่ถ้ามันไม่จริง เราก็อาจจะต้องทำไปเรื่อย ๆ เรื่อย ๆ ... เหมือนกับ ไม่มีทางรู้เลย ว่ามันเป็นจริงรึเปล่า"

ส่วนในกรณีของ H(X, Y) ที่สามารถสร้างได้ ...

"ถ้า X(Y) หยุดการทำงาน เราก็จะได้คำตอบจาก H(X, Y) แต่ถ้า X(Y) ไม่หยุดการทำงาน H(X, Y) ก็จะทำงานไปเรื่อย ๆ ... ไม่มีทางรู้ว่ามันจะหยุดรึเปล่า"

จบละ

Transformation Matrix: ผลคูณภายใน

เรื่องนี้เป็นภาคต่อของ Transformation Matrix: พื้นฐาน นะ ไม่ยากเหมือนตอนที่แล้ว ๆ มา

เราจะเริ่มที่เรื่องของ ผลคูณภายใน ก่อน แต่คราวนี้ จะคิดกรณีของจำนวนเชิงซ้อนด้วย

สมมติว่าเรามีเวกเตอร์ u อยู่ เราคิดว่า ค่าในแต่ละมิติของ u เป็นฟังก์ชันของเลขมิติ (เหมือนกับในตอน Discrete: ฟังก์ชัน เวกเตอร์ และเมตริกซ์) คือ

u = (u(1), u(2), u(3), ..., u(n))

แต่เดิม เราคิดว่าผลคูณภายในของ u กับ v ที่มีมิติเป็น n เท่ากัน คือ

u ⋅ v = Σ_1≤i≤n u(i)v(i)

ดังนั้น ขนาดของ u สามารถหาได้จาก (คราวนี้ขอเขียนว่า |u| นะ)

|u|² = u ⋅ u = Σ_1≤i≤n u(i)²

หรือก็คือ

|u| = (u ⋅ u)^1/2

แต่ ถ้าเกิด u(i) เป็นจำนวนเชิงซ้อนหละ ... u ⋅ u อาจจะไม่ใช่จำนวนจริงก็ได้ แล้ว |u| ก็อาจจะมีได้ 2 ค่าน่ะสิ (จากสมการ |u|² = u ⋅ u)

เราแก้ปัญหานี้ได้ โดยนิยามอะไรใหม่นิดนึง ... ถ้าเรากำหนดให้ สังยุกต์ (Conjugate) ของเวกเตอร์ เป็นแบบนี้

u^* = (u(1)^*, u(2)^*, u(3)^*, ..., u(n)^*)

พอเราหา u^* ⋅ u ผลก็คือ

u^* ⋅ u = Σ_1≤i≤n u(i)^*u(i)

จากความรู้เรื่องจำนวนเชิงซ้อน เรารู้ว่า ถ้า z เป็นจำนวนเชิงซ้อนใด ๆ แล้ว z^*z = |z|² เป็นจำนวนจริง ดังนั้น u^* ⋅ u ของเรา ก็จะเป็นจำนวนจริงด้วย

เราเลยนิยาม ผลคูณภายใน ใหม่ แบบนี้

u ⋅ v แบบใหม่ = u^* ⋅ v แบบเก่า

แต่ u ⋅ v แบบใหม่ มีคุณสมบัติต่างกับแบบเก่าด้วย คือ

u ⋅ v ≠ v ⋅ u (หมายถึง ไม่จำเป็นต้องเท่ากันเสมอไป)
แต่ u ⋅ v = (v ⋅ u)^* เสมอ

เมื่อคิดเวกเตอร์เป็นเมตริกซ์แนวตั้ง

ถ้าเรามอง u เป็นเมตริกซ์มิติ n × 1 เราก็ยังเขียนว่า

u = (u(1), u(2), u(3), ..., u(n))

ได้เหมือนเดิม ... แต่เดี๋ยวลองกำหนด u^* ใหม่ ให้เป็นแบบนี้

u^* = [u(1)^* u(2)^* u(3)^* ... u(n)^*]

หรือก็คือ

u^* แบบใหม่ = (u^*)^T แบบเก่า

พอเราหาผลคูณแบบเมตริกซ์ของ u^* กับ v ก็จะได้ผลเป็น เมตริกซ์มิติ 1 × 1 แบบนี้

u^*v = [u ⋅ v]

เพื่อให้เขียนง่ายขึ้น เราจะถือซะว่า เมตริกซ์มิติ 1 × 1 เป็นจำนวนเชิงซ้อนตัวเดียวเลยละกัน ... มันจะเป็น

u^*v = u ⋅ v

ผลคูณภายในของเมตริกซ์กับเมตริกซ์

เราลองใช้นิยามผลคูณภายในอย่างเดียวกันกับเมตริกซ์ดู เราจะหาขนาดของเมตริกซ์ได้รึเปล่านะ?

A ⋅ A = A^*A = ?

ถ้าเรามองว่า A เป็นเมตริกซ์ที่มีมิติ m × n ซึ่งประกอบด้วยเวกเตอร์แนวตั้ง แบบนี้

A = [A₁ : A₂ : A₃ : ... : A_m]

A^* จะเป็นเมตริกซ์ที่มีมิติ n × m หน้าตาแบบนี้

A^* = (A₁^* : A₂^* : A₃^* : ... : A_m^*)

เผื่อลืม: รูปการคูณเมตริกซ์

เอามาจาก Transformation Matrix: พื้นฐาน นะ

ดังนั้นค่าของ A^*A จะเป็นเมตริกซ์มิติ n × n แบบนี้

B = A^*A
B_i,j = A_i ⋅ A_j

เมื่อ B_i,j คือ ค่าในแถวที่ i หลักที่ j ของ B

คราวนี้ คุณสมบัติสำคัญก็คือ

A_i ⋅ A_j = (A_j ⋅ A_i)^*

ซึ่งทำให้

B_i,j = B_{j, i}^*

ซึ่งแปลว่า

B = B^*

เราเรียกเมตริกซ์ที่มีคุณสมบัตินี้ว่า เมตริกซ์เฮอร์มิเชียน (Hermitian Matrix)

ไป ๆ มา ๆ เราก็ไม่ได้ขนาดของ A แฮะ แต่ได้คุณสมบัติที่ว่า A ⋅ A เป็นเมตริกซ์เฮอร์มิเชียนแทน

แล้ว แต่ละค่า B_i,j มันมีความหมายว่ายังไงหละ?

ถ้าเวกเตอร์ A_i ตั้งฉากกันทุกคู่

ดังนั้น A_i ⋅ A_j จะเป็น 0 เมื่อ i ≠ j

มันก็แปลว่า B_i,j = 0 เมื่อ i ≠ j น่ะสิ

A ⋅ A ก็จะเป็น เมตริกซ์ทแยงมุม (Diagonal Matrix)!!!

เราจะเขียนได้ว่า ... (สัญลักษณ์แบบนี้ เอามาจาก Transformation Matrix: Eigenvalues & Eigenvectors "ตอนแรก" นะ)

A ⋅ A = [ B_1,1 \ B_2,2 \ B_3,3 \ ... \ B_n,n ]

เนื่องจาก B_i,i = A_i ⋅ A_i = |A_i|² เป็นจำนวนจริง ดังนั้น

A ⋅ A เป็นเมตริกซ์จำนวนจริงด้วย

เรื่องของ Determinant

ถ้า A เป็นเมตริกซ์จัตุรัส เราจะหา det(A) ได้

เนื่องจาก det(A) เกิดจากการเอาค่า A มาคูณกับบวกกัน ดังนั้น

det(A^*) = det(A)^*

ดังนั้น เราก็เลยรู้แน่ ๆ ว่า

det(A ⋅ A) เป็นจำนวนจริง

เพราะว่า

det(A ⋅ A) = det(A^*A) = det(A)^*det(A)

เป็นจำนวนจริงแน่นอน

ดังนั้น เราอาจจะนิยาม ขนาดของ A อีกแบบนึง ซึ่งเป็นจำนวนจริงไม่ติดลบเสมอ ดังนี้

|A| = det(A ⋅ A)^1/2

ซึ่งสิ่งที่เราได้เพิ่มมาอีกอย่างก็คือ ... A ไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัสก็ได้น่ะสิ !!!

Transformation Matrix: Eigenvalues & Eigenvectors "การคำนวณ"

พล่ามเรื่อง eigenvalue กับ eigenvector ไปเยอะละ แต่ยังไม่ได้บอกเลย ว่าเราจะหามันได้ยังไง :P คิดว่าถึงเวลาแล้วหละ มาลองดูกันดีกว่า

Analytical Solution

จำได้มั้ยว่า ใน Transformation Matrix: Eigenvalues & Eigenvectors "คุณสมบัติ" เรารู้มาอย่างนึงว่า

λ จะเป็น eigenvalue ของ A ก็ต่อเมื่อ det(A - λI) = 0

ดังนั้น เราก็ตั้งต้นด้วยสมการ

det(A - λI) = 0

สมการนี้ มักจะเรียกกันว่า "Characteristic Equation" ของปัญหาการหา eigenvalue และ eigenvector นี้ ส่วนพหุนาม P(λ) = det(A - λI) ก็จะเรียกว่า "Characteristic Polynomial"

ถ้า A มีมิติเป็น n × n เราจะรู้ว่า det(A - λI) เป็นพหุนามดีกรี n อย่างแน่นอน ดังนั้น เราจะสามารถหา eigenvalue λ ได้ n ตัว (นับตัวซ้ำด้วย)

คราวนี้ พอเราเอา λ แต่ละตัว ไปแทนใน

(A - λI)e = 0

จะได้ระบบสมการที่มี n สมการ และมีตัวแปร n ตัว ซึ่งมีคุณสมบัติ linear dependency (เพราะว่า det เป็น 0) ดังนั้น เซตของคำตอบจะมีจำนวนนับไม่ถ้วน ซึ่งก็ถูกต้อง เพราะว่า eigenvector มีจำนวนเป็นอนันต์

แต่ถ้าหาก λ ที่เลือกไปแทนในสมการ (A - λI)e = 0 นั้น ไม่ใช่รากซ้ำจากการแก้สมการ P(λ) = 0 เราจะรู้ว่า eigenvector ทั้งหมดที่ได้จะมีทิศขนานกัน

Eigenvalue ของเมตริกซ์สมมาตรที่มีสมาชิกเป็นจำนวนจริง เป็นจำนวนจริง

รู้สึกว่ากรณี A = A^T นี่จะพูดบ่อยจังเนอะ :D

วิธีพิสูจน์อันนี้ อาจจะดูแปลก ๆ หน่อย แต่ทุกขั้นตอนก็จำเป็นนะ เราจะเริ่มโดยสมมติว่า e เป็น eigenvector ที่อาจจะมีค่าที่ไม่ใช่จำนวนจริงก็ได้ เราจะพิสูจน์ว่า λ ซึ่งเป็น eigenvalue ของมัน ต้องเป็นจำนวนจริง

เราจะเขียน e^* เพื่อหมายถึง เมตริกซ์ conjugate transpose ของ e ซึ่งก็คือ เอาค่าในแต่ละมิติของ e^T ไปเปลี่ยนเป็น conjugate ของมัน

คราวนี้ ผลคูณภายในของเวกเตอร์เชิงซ้อน u กับ v ใด ๆ เราก็จะเขียนเป็น u^*v แทน u ⋅ v

เริ่มพิสูจน์โดยการหา e ⋅ Ae ...

e^*Ae = λ ||e||²

คราวนี้ ลองใส่ * เข้าไปทั้งสองข้าง

(e^*Ae)^* = (λ ||e||²)^*

ใช้คุณสมบัติที่ว่า (XY)^* = Y^*X^* กระจายเครื่องหมาย * ในฝั่งซ้าย ส่วนฝั่งขวา กระจายแค่ conjugate เข้าไปที่ λ เพราะว่า ||e||² เป็นจำนวนจริงอยู่แล้ว จะได้ว่า

e^*A^*e = λ^* ||e||²

แต่จากเงื่อนไขที่ว่า A เป็นเมตริกซ์จำนวนจริง และสมมาตร เราเลยรู้ว่า A = A^* ซึ่งทำให้

e^*Ae = λ^* ||e||²

ฝั่งซ้ายของสมการนี้ เท่ากับฝั่งซ้ายของสมการข้างบน (กลับไปดูสิ) พอจับมันมาเท่ากัน เราจะได้

λ ||e||² = λ^* ||e||²
λ = λ^*

สรุปได้แล้วว่า λ ต้องเป็นจำนวนจริง

ข้อจำกัดของ Analytical Solution

เนื่องจาก เราสามารถคำตอบเชิงวิเคราะห์ (Analytical Solution) ของสมการ P(λ) = 0 ได้ก็ต่อเมื่อ n ≤ 4 (ความจริงข้อนี้ พิสูจน์ยากมาก ๆ ... ขอยกมาเฉย ๆ ละกัน) ดังนั้น ในกรณีที่ n > 4 เราจะต้องหาวิธีทางตัวเลข (Numerical Method) เพื่อแก้สมการนี้

การหารากของสมการพหุนามแบบ numerical เนี่ย มันก็มีอยู่หลายวิธีแหละ แต่ ... จริง ๆ ถ้าเราจะหา numerical method อยู่แล้ว เราลองหาจากปัญหาต้นแบบได้มั้ย? แบบที่ไม่ต้องยุ่งกับ P(λ) หนะ

Numerical Solution

วิธีที่จะบอกเนี่ย เป็นหลักการเบื้องต้นนะ ในการใช้งานจริง ต้องมีการปรับปรุง เปลี่ยนแปลง อีกเยอะเลย

เริ่มละนะ ... สมมติว่าเรามีเวกเตอร์อะไรก็ไม่รู้ เส้นนึง ชื่อว่า u แล้วก็ สมมติว่า eigenvector ของเรา มีอยู่ n ตัว คือ e₁ e₂ e₃ ... e_n และ eigenvalue ก็คือ λ₁ λ₂ λ₃ ... λ_n ตามลำดับ

เนื่องจาก ตัวเลขห้อย e กับ λ มันจะเรียงกันยังไงก็ได้ เราก็สมมติซะว่า

λ₁ ≥ λ₂ ≥ λ₃ ≥ ... ≥ λ_n

ละกัน ... จากนั้น ก็สมมติว่า a_i เป็นผลจากการลองหาค่า Au แบบนี้

Au = a₁e₁ + a₂e₂ + a₃e₃ + ... + a_ne_n

สมมติว่า a₁ ≠ 0 ก่อนนะ คราวนี้ เราลองเอา A ใส่เข้าไปอีกที ทั้งสองข้างของสมการ ผลจะเป็น

A²u = λ₁a₁e₁ + λ₂a₂e₂ + λ₃a₃e₃ + ... + λ_na_ne_n

ถ้าเอา A ใส่ซ้ำไปเรื่อย ๆ มันจะเป็น ...

A^p+1u = λ₁^pa₁e₁ + λ₂^pa₂e₂ + λ₃^pa₃e₃ + ... + λ_n^pa_ne_n

คราวนี้ ถ้าหาก λ₁ > λ₂ ... ลองดึง λ₁ ออกมาจากสัมประสิทธิ์ทุกตัวสิ

A^p+1u = λ₁^p(a₁e₁ + (λ₂/λ₁)^pa₂e₂ + (λ₃/λ₁)^pa₃e₃ + ... + (λ_n/λ₁)^pa_ne_n)

พอเราให้ p → ∞ แล้ว เราจะเห็นว่า (λ_i/λ₁)^p เป็น 0 หมดทุกตัวยกเว้นเมื่อ i = 1 ดังนั้นข้อสรุปของเราก็คือ

A^p+1u ≈ λ₁^pa₁e₁

แสดงว่า การเอา A คูณซ้ำ ๆ ไปเรื่อย ๆ จะทำให้เราได้ e₁ ออกมาเอง

แต่ ถ้าหาก λ₁ = λ₂ = λ₃ = ... = λ_m หละ? (m ≤ n นะ) ... เราก็ดึงตัวร่วมออกจากทุกตัวได้อยู่ดีนะ มันจะเป็นงี้

จาก A^p+1u = λ₁^p(a₁e₁ + (λ₂/λ₁)^pa₂e₂ + (λ₃/λ₁)^pa₃e₃ + ... + (λ_n/λ₁)^pa_ne_n)

แต่ λ₁ = λ₂ = λ₃ = ... = λ_m > λ_m+1 (ถ้า m = n ก็ถือซะว่า λ_n+1 = 0 ไปเลย) ดังนั้น

A^p+1u = λ₁^p(a₁e₁ + a₂e₂ + a₃e₃ + ... + a_me_m
+ (λ_m+1/λ₁)^pa_m+1e_m+1 + (λ_m+2/λ₁)^pa_m+2e_m+2 + (λ_n/λ₁)^pa_ne_n)

ซึ่ง เมื่อ p → ∞ เราจะได้ว่า

A^p+1u ≈ λ₁^p(a₁e₁ + a₂e₂ + a₃e₃ + ... + a_me_m)

ผลลัพธ์ที่ได้เป็นเวกเตอร์ a₁e₁ + a₂e₂ + a₃e₃ + ... + a_me_m ซึ่งเรารู้ว่า มันก็เป็น eigenvector เหมือนกัน เพราะว่า eigenvalue มันเท่ากัน (พิสูจน์ไปแล้วในหัวข้อย่อย "จริง ๆ แล้ว จำนวน Eigenvector เป็นอนันต์" ในเรื่อง Transformation Matrix: Eigenvalues & Eigenvectors "คุณสมบัติ")

ดังนั้น เราจึงสรุปได้ว่า การเอาเวกเตอร์ที่เราสุ่มขึ้นมา คูณด้วย A ไปเรื่อย ๆ เราจะได้ eigenvector ตัวที่มีค่า eigenvalue สูงสุดออกมาเอง

มีอีกเรื่องที่ยังคาใจเราอยู่นะ คือ เมื่อตอนแรก เราสมมติว่า a₁ ≠ 0 ... แล้วถ้า a₁ = 0 มันจะเป็นยังไงน่ะเหรอ? เราก็คิดที่ a₂ แทนสิ ... ผลลัพธ์ก็คือ eigenvector ที่มี eigenvalue มากเป็นอันดับรองลงมาไงหละ

ดังนั้น ถ้าเรามั่วเวกเตอร์ u มาครั้งแรก แล้วเราหา e₁ ได้แล้ว เราก็มั่ว u มาอีกตัวที่ทำให้ a₁ = 0 ซะ คราวนี้ เราก็จะได้ e₂ แทน ... ทำซ้ำไปเรื่อย ๆ เราก็จะได้ e_i ครบทุกตัว

ในทางปฏิบัติ ทุกครั้งที่เราเอา A มาคูณ เราควรจะ normalize ผลลัพธ์ด้วย เพื่อให้ขนาดของเวกเตอร์ ไม่ใหญ่เกินไป จนเกิดปัญหา overflow

ผลพลอยได้จากปัญหา Eigenvector

มีคนเค้าพิสูจน์ไว้แล้วว่า ถ้าเราสมมติ P(λ) เป็นพหุนามดีกรี n ที่มีสัมประสิทธิ์เป็นจำนวนจริง ขึ้นมาอันนึง เราจะสามารถหา A ที่ทำให้ P(λ) = det(A - λI) ได้เสมอ

ดังนั้น ... แทนที่เราจะใช้ numerical method สำหรับหารากของสมการพหุนาม มาแก้ปัญหา eigenvector เราก็สามารถทำกลับกันได้ โดนเปลี่ยนปัญหาการหารากของสมการพหุนาม ไปเป็นปัญหา eigenvector แล้วใช้วิธีอย่างเมื่อกี๊

แปลว่า เราได้ numerical method สำหรับหารากของสมการพหุนาม เพิ่มขึ้นอีกวิธี ก็คือ วิธีการหา eigenvector นี่เอง

ทิ้งท้าย

จริง ๆ แล้ว numerical method สำหรับหา eigenvector เนี่ย มันมีอีกหลายวิธีมาก ๆ แต่ที่ยกมาให้ดูเนี่ย อยากให้เห็นวิธีการประยุกต์ความรู้มากกว่า (มันไม่ยาก แต่ใช้งานได้)

Transformation Matrix: Eigenvalues & Eigenvectors "คุณสมบัติ"

ขอกำหนดข้อตกลงบางอย่างก่อนนะ ไม่อยากจะเขียนอะไรยั้วเยี้ย ...

• A เป็นเมตริกซ์จัตุรัสที่มีมิติเท่ากับ n × n และมี eigenvector
• A_i คือเวกเตอร์ของ แถว ที่ i ของ A (สังเกตว่า แถว เรียงอยู่ในแนวนอน แต่ถือว่า A_i เป็นเมตริกซ์แนวตั้ง) ดังนั้น A = ( A₁ : A₂ : A₃ : ... : A_n )

เผื่อลืม: ถ้าไม่รู้ว่าสัญลักษณ์ ( A₁ : A₂ : A₃ : ... : A_n ) คืออะไร ไปดูที่ Transformation Matrix: พื้นฐาน นะ

คุณสมบัติพื้นฐาน ที่สำคัญ ๆ ของ eigenvalue และ eigenvector ก็คือ

λ เป็น Eigenvalue ของ A ก็ต่อเมื่อ det(A - λI) = 0

สมมติว่า u เป็น eigenvector ของ A และมี eigenvalue เป็น λ จากนิยาม เราจะรู้ว่า

Au = λu
Au - λu = 0

จาก Iu = u

Au - λIu = 0

จากคุณสมบัติการกระจายของเมตริกซ์

(A - λI)u = 0

ได้ระบบสมการเชิงเส้น n ตัวแปร ที่พจน์ของค่าคงที่ทางขวาเป็น 0 หมด

เนื่องจากเราสนใจเฉพาะกรณี u ≠ 0 แสดงว่า สามารถเลือก u ที่ทำให้ (A - λI)u = 0 ได้ มันก็แปลว่า

เซตของเวกเตอร์ n เส้น จากแต่ละแถวของ A - λI มีคุณสมบัติ linear dependency

ซึ่งประโยคนี้ เทียบเท่ากับ

det(A - λI) = 0

เผื่อลืม: เรื่องของ det กับคุณสมบัติ linear dependency มีอยู่ใน 3 เรื่องนี้นะ

1. ตามหาความหมายของ Determinant: Linear Combination
2. Discrete: Linear Dependency
3. Continuous: Linear Dependency

ตอนนี้เราพิสูจน์ "ถ้า ... แล้ว" ได้เรียบร้อยละ การจะพิสูจน์ย้อนกลับก็ง่าย ๆ นะ ทำจากล่างขึ้นบนก็ได้เลย เพราะมันเป็น "ก็ต่อเมื่อ" ทุกขั้น ไม่เขียนให้ดูละกัน

จริง ๆ แล้ว จำนวน Eigenvector เป็นอนันต์

เหมือนกับโกหกกันไปแล้วทีนึงนะ ว่าปกติ จะมี eigenvector อยู่ (ไม่เกิน) n เส้น ... :P

จริง ๆ มันก็ไม่ใช่โกหกอะนะ เพราะมีคำว่า "ปกติ" อยู่ :D ... จริง ๆ มันขึ้นกับนิยามมากกว่าแหละ ลองดูนี่สิ

Au = λu

ถ้าเราเอาจำนวนจริง c ≠ 0 คูณเข้าไปทั้งสองข้าง

cAu = cλu

จากคุณสมบัติพื้นฐานของเมตริกซ์และเวกเตอร์ ...

A(cu) = λ(cu)

เห็นมั้ยว่า ถ้า u เป็น eigenvector แล้ว cu ก็เป็น eigenvector แต่ว่าเวกเตอร์พวกนี้มันขนานกัน บางคนก็เลยไม่สนใจไง ถือว่ามันเป็นพวกเดียว ๆ กัน นับ 1 (หรือจะบอกว่า นับแต่ unit eigenvector ก็ได้)

แต่มันก็มีความไม่ปกติที่ไม่ได้มาจากนิยามด้วยนะ ลองดูกรณีที่ eigenvector สองตัวมี eigenvalue เท่ากันซักหน่อย ...

Au = λu
Av = λv
⇓
A(pu + qv) = λ(pu + qv)
ดังนั้น pu + qv ก็เป็น eigenvector

ผลรวมเชิงเส้นของ eigenvector พวกนี้ ก็เป็น eigenvector หมดเลย!!!

แนะแนวการมอง

สมมติว่า E เป็นเซตของ eigenvector ทั้งหมดของ A และเราต้องการเลือก eigenvector กลุ่มนึง (ให้เป็นเซต S) ซึ่งมีคุณสมบัติว่า span(E) = span(S) และจำนวนสมาชิกของ S น้อยที่สุด

คุณสมบัติที่สำคัญอย่างแรกของ E (และ S) ก็คือ ถ้า x ∈ span(E) แล้ว Ax ∈ span(E) ด้วย เพราะว่า

A(a₁e₁ + a₂e₂ + a₃e₃ + ... + a_me_m)
= a₁Ae₁ + a₂Ae₂ + a₃Ae₃ + ... + a_mAe_m
= λ₁a₁e₁ + λ₂a₂e₂ + λ₃a₃e₃ + ... + λ_ma_me_m ∈ span(E)
เมื่อ m = | E |

ถ้า A เป็นเมตริกซ์สมมาตรแล้ว x จะตั้งฉากกับ e ∈ E ก็ต่อเมื่อ Ax ตั้งฉากกับ e

ถ้า A เป็นเมตริกซ์สมมาตร เราจะรู้ว่า

A = A^T

สมมติว่า e เป็น eigenvector ที่มี eigenvalue เป็น λ เราจะรู้ว่า

Ae = λe

แล้วก็สมมติอีกว่า x เป็นเวกเตอร์ที่ตั้งฉากกับ e

x ⋅ e = 0

เพื่อให้เขียนง่ายขึ้น เราจะเขียนแทนผลคูณภายในด้วยการคูณเมตริกซ์ แบบนี้ ...

x^Te = 0

จากสมการแรก ถ้าเราเอา x^T คูณทางซ้าย จะได้เป็น

x^TAe = λx^Te
x^TAe = 0

ซึ่ง ถ้าใส่ transpose เข้าไป จะกลายเป็น

e^TA^Tx = 0

แต่เนื่องจาก A = A^T ดังนั้น

e^TAx = 0

แสดงว่า Ax ตั้งฉากกับ e ด้วย

ส่วนการพิสูจน์ย้อนกลับว่า "ถ้า Ax ตั้งฉากกับ e แล้ว x ตั้งฉากกับ e ด้วย" ก็ทำย้อนกลับได้ง่าย ๆ เหมือนกัน ... ไม่เขียนให้ดูแล้วนะ

การสร้าง Orthonormal Basis จาก Eigenvector

จริง ๆ เราสามารถหาเซต S ของ eigenvector ที่ตั้งฉากกันและเป็น basis ที่สมบูรณ์ (span(S) = span(E)) ได้จากแนวคิดที่แล้ว โดยคิดว่า ถ้าเราหา eigenvector ได้แล้วตัวนึง เราก็ตัดเวกเตอร์ทั้งหมดที่ไม่ตั้งฉากกับ eigenvector ตัวนั้นทิ้งจากการพิจารณาได้ ดังนั้น eigenvector ตัวต่อ ๆ ไปที่หาได้ มันจะตั้งฉากกับตัวก่อนหน้าทั้งหมด

ที่เอามาให้ดูต่อไปนี้ เป็นอีกวิธีนึงสำหรับพิสูจน์ การมีอยู่จริงของ orthonormal basis จาก eigenvector โดยใช้หลักการที่ว่า ถ้าเซต S ของ eigenvector ยังไม่เป็น basis ที่สมบูรณ์ (คือ span(S) ≠ span(E)) เราจะสามารถหา e ∈ E - S ที่ตั้งฉากกับสมาชิกทุกตัวใน S ได้

สมมติว่า u กับ v เป็น eigenvector สองตัวที่มี eigenvalue เป็น λ กับ μ ตามลำดับ

Au = λu
Av = μv

เติมผลคูณภายในเข้าไปแบบนี้

v^TAu = λv^Tu
u^TAv = μu^Tv

เอาอันล่างมา transpose จะได้

v^TA^Tu = μv^Tu

เนื่องจาก A = A^T ฝั่งซ้ายของสมการนี้ จะไปเท่ากับสมการข้างบน ดังนั้น

λv^Tu = μv^Tu

ซึ่งแปลว่า λ = μ หรือ v^Tu = 0

ถึงตรงนี้ บางคนอาจจะเห็นว่า มันคล้าย ๆ กับบทพิสูจน์เรื่องที่แล้วเลย ... ถูกแล้วหละ จริง ๆ มันคืออันเดียวกันเลย

ถ้า v^Tu = 0 มันก็แปลว่า u ตั้งฉากกับ v อยู่แล้ว ... ส่วนอีกกรณีนึง ...

ถ้า λ = μ

เราพิสูจน์ไปแล้วว่า

w = pu + qv จะเป็น eigenvector ด้วย

ซึ่งถ้า u กับ v ไม่ขนานกัน เราจะสามารถหา w ที่ตั้งฉากกับ u ได้แน่ ๆ

Transformation Matrix: Eigenvalues & Eigenvectors "ตอนแรก"

ถ้าใครช่างสังเกตหน่อย จะเห็นว่า ผมเปลี่ยนชื่อหัวข้อไปนิดนึง จากที่วางแผนไว้ใน Tunoblog Summarized จาก ...

เดิม Transformation: Eigenvalues & Eigenvectors
เป็น Transformation Matrix: Eigenvalues & Eigenvectors (คงมีหลายตอน)

จริง ๆ มันเป็นตั้งแต่ตอนที่แล้วแล้วแหละ (Transformation Matrix: Orthonormal Transformations) แต่ก็ยังไม่ลบชื่อหัวข้อเดิมออก ... มันเป็นความจงใจหนะนะ คือ จะเขียนต่ออีก ... ตอนนี้ขอเข้าเรื่องก่อน

นิยามของ Eigenvalue และ Eigenvector

ขอบอกนิยามสำหรับกรณีเมตริกซ์จัตุรัสมิติจำกัดก่อนนะ กรณีที่ทั่วไปมากขึ้น จะพูดถึงในตอนถัด ๆ ไป

Eigenvalues & Right Eigenvectors

ให้ A เป็นเมตริกซ์จัตุรัส มิติ n × n
และให้ u เป็นเวกเตอร์ n มิติ (คือ เมตริกซ์แนวตั้ง มิติ n × 1 หนะ)
ถ้าสามารถหาจำนวนจริง λ ที่ไม่ใช่ 0 ที่ทำให้
Au = λu ได้
จะเรียก u ว่าเป็น Eigenvector ทางขวา ของ A
และจะเรียก λ ว่าเป็น Eigenvalue ของ u

ที่เอานิยามแบบนี้มาให้ดู เพราะมันเป็นความนิยมหนะ จริง ๆ แล้ว ถ้าเราให้ u เป็นเมตริกซ์แนวนอน มิติ 1 × n และเปลี่ยนเงื่อนไขของสมการเป็น

uA = λu

เราก็จะเรียก u ว่าเป็น Eigenvector ทางซ้าย ของ A

เรื่องมหัศจรรย์มีอยู่ว่า ... λ มันจะเท่ากันทั้งสองกรณีน่ะสิ

เมตริกซ์ของ Eigenvalue และ เมตริกซ์ของ Eigenvector

ตอนนี้ ขอเรียก eigenvector ทางซ้ายว่า eigenvector เฉย ๆ นะ จะได้สั้น ๆ และตรงตามความนิยม

"โดยทั่วไป" แล้ว เมตริกซ์ n × n จะมี eigenvector อยู่ n ตัว ดังนั้น eigenvalue ก็จะมีอยู่ n ตัวด้วย

สมมติว่า n = 3 ก่อนละกันนะ แล้วก็ให้ λ₁ λ₂ λ₃ เป็น eigenvalue ทั้งสามของ เมตริกซ์ A ที่มีมิติ 3 × 3

เราจะเขียนเมตริกซ์ของ eigenvalue เป็นเมตริกซ์ทแยงมุมดังนี้

D₁ = (λ₁, 0, 0)
D₂ = (0, λ₂, 0)
D₃ = (0, 0, λ₃)
D = [ D₁ : D₂ : D₃ ]

เพื่อให้เขียนง่าย ๆ หน่อย ขอย่อเมตริกซ์ทแยงมุมเป็นแบบนี้นะ

D = [ λ₁ \ λ₂ \ λ₃ ]

ส่วนเมตริกซ์ของ eigenvector ก็แค่เอา eigenvector มาต่อกัน มันก็จะได้เมตริกซ์จัตุรัสเอง ... หน้าตาแบบนี้

P = [ u₁ : u₂ : u₃ ]

Eigen Decomposition

แล้วไอ้เมตริกซ์เมื่อกี๊ มันเอาไว้ทำอะไรอะ?

เดี๋ยวจะเอาให้ดู ว่าประโยชน์มันคืออะไร

สมมติก่อนว่า A เป็นเมตริกซ์ที่มีมิติเป็น 3 × 3 ซึ่งมี eigenvector 3 เส้น คือ u₁ u₂ u₃ และ eigenvector ทั้งสาม จับคู่กับ eigenvalue 3 ค่า คือ λ₁ λ₂ λ₃ ตามลำดับ ... จากนั้น กำหนดให้

D = [ λ₁ \ λ₂ \ λ₃ ]
P = [ u₁ : u₂ : u₃ ]

เราจะรู้ว่า

AP = A[ u₁ : u₂ : u₃ ]
AP = [ Au₁ : Au₂ : Au₃ ]
AP = [ λ₁u₁ : λ₂u₂ : λ₃u₃ ]

และ

PD = [ u₁ : u₂ : u₃ ][ λ₁ \ λ₂ \ λ₃ ]
PD = [ λ₁u₁ : λ₂u₂ : λ₃u₃ ]

ดังนั้น

AP = PD
A = PDP^-1

การยกกำลังเมตริกซ์ด้วย Eigen Decomposition

อันนี้เป็น หนึ่งในการใช้งานที่สุดแสนจะคลาสสิก และง่ายด้วย ... ความรู้ที่ต้องใช้ก็คือ

[ λ₁ \ λ₂ \ λ₃ ]ⁿ = [ λ₁ⁿ \ λ₂ⁿ \ λ₃ⁿ ] เมื่อ n เป็นจำนวนเต็มใด ๆ

คราวนี้ สมมติว่าเราอยากหา Aⁿ เราก็แตกด้วย Eigen Decomposition ก่อน แล้วทำแบบนี้

A = PDP^-1
A² = PDP^-1 PDP^-1 = PD²P^-1
A³ = PD²P^-1 PDP^-1 = PD³P^-1
...
Aⁿ = PDⁿP^-1

เนื่องจาก Dⁿ มันหาได้ง่าย ๆ จากสมการข้างบน ดังนั้น วิธีนี้จึงมีประสิทธิภาพสูงกว่าการคูณมันไปเรื่อย ๆ ตรง ๆ เห็น ๆ

นอกจากนี้ อินเวอร์สของ A ก็หาได้ด้วยวิธีเดียวกัน ... แบบนี้

Aⁿ = PDⁿP^-1
I = PDⁿP^-1A^-n
P^-1 = DⁿP^-1A^-n
D^-nP^-1 = P^-1A^-n
PD^-nP^-1 = A^-n

ดังนั้น สมการ Aⁿ = PDⁿP^-1 ก็เลยใช้ได้กับจำนวนเต็ม n ใด ๆ ไม่จำกัดเฉพาะจำนวนเต็มบวก (เป็น 0 ก็ได้นะ)

คราวนี้ พอเราหาเมตริกซ์ยกกำลังได้สะดวก ๆ แล้ว พหุนามของเมตริกซ์ก็เขียนได้ง่าย ๆ เหมือนกัน

สมมติว่า f(A) เป็นพหุนามของ A
ถ้าเราสามารถแยก A = PDP^-1 ได้ เราจะรู้ว่า
f(A) = P f(D) P^-1
ซึ่งทำให้ f(A) = P [ f(λ₁) \ f(λ₂) \ f(λ₃) \ ... \ f(λ_n) ] P^-1

พอรู้หยั่งงี้ ฟังก์ชันสุดฮิต e^x ของเรา ก็ใช้กับเมตริกซ์ได้แล้ว เพราะว่า เราสามารถเขียนให้อยู่ในรูปของพหุนามได้ ดังนี้

e^A = 1 + A + A²/2! + A³/3! + ...

ดังนั้น ถ้าเราแทนค่า e^A = f(A) ในความสัมพันธ์ f(A) = P [ f(λ₁) \ f(λ₂) \ f(λ₃) \ ... \ f(λ_n) ] P^-1 จะได้ว่า

e^A = P [ e^λ₁ \ e^λ₂ \ e^λ₃ \ ... \ e^λ_n ] P^-1

และที่ยิ่งไปกว่านี้ ... หน้าตาแบบนี้ ทำไมมันจะใช้ได้แค่ e หละ? ... ขยายต่อสิ ให้ฐานมันเป็นจำนวนจริงอะไรก็ได้

a^A = P [ a^λ₁ \ a^λ₂ \ a^λ₃ \ ... \ a^λ_n ] P^-1

เห็นมั้ย ว่าใช้เมตริกซ์เป็นเลขชี้กำลังได้ละ :D ผลลัพธ์เป็นเมตริกซ์ด้วย

จริง ๆ เราจะนิยามสัญลักษณ์ B^A เมื่อ A กับ B เป็นเมตริกซ์ อีกก็ได้นะ ก็แค่เอา B ไปแทนที่ a ในสมการข้างบนนี่ ... แต่ ... มันจะดูแปลก ๆ อ๊ะป่าว ??? ... เมตริกซ์ที่มีข้อมูลในช่องเป็นเมตริกซ์ ...

---

และแล้วก็จบตอนแรกของเรื่อง eigenvalue กับ eigenvector ... ยังมีอีกเยอะเลยหละ แต่ค่อย ๆ เอามาให้ดูละกัน จะได้อ่านกันไหว

Transformation Matrix: Orthonormal Transformations

พูดเรื่องคำศัพท์นิดนึงก่อน มาดูว่า คำว่า "Normal" เนี่ย มันมีความหมายประมาณไหน

สมมติว่าเรามีเวกเตอร์ v อยู่ ขนาดของมัน เรียกว่า Norm เขียนแทนด้วย || v || (หรือ | v |)

Unit Vector คือ เวกเตอร์ที่มีขนาดเป็น 1 ภาษาไทยเรียกตรง ๆ ว่า เวกเตอร์หนึ่งหน่วย

Normalization คือ การหารเวกเตอร์ด้วยขนาดของมันเอง (เช่น v / || v ||) ผลลัพธ์เป็น unit vector ที่มีทิศทางเดิม

อีกที่นึงที่เจอคำว่า "Normal" บ่อย ๆ

ใน 2 มิติ Normal Vector ของเส้นตรง คือ เวกเตอร์ที่มีทิศตั้งฉากกับแนวเส้นตรงนั้น

ใน 3 มิติ Normal Vector ของระนาบ คือ เวกเตอร์ที่มีทิศตั้งฉากกับระนาบนั้น

รู้สึกอันนี้ คำว่า normal มันจะไม่ค่อยเกี่ยวกันเท่าไหร่แฮะ

ถ้า r(s) เป็นฟังก์ชันจาก เซตย่อยของจำนวนจริง ไปยังเซตย่อยของปริภูมิใด ๆ และมีอนุพันธ์อันดับสอง

T(s) = r'(s) / || r'(s) || เรียกว่า Tangent Vector
N(s) = T'(s) / || T'(s) || เรียกว่า Normal Vector
B(s) = T(s) × N(s) เรียกว่า Binormal Vector

อันนี้เกี่ยวกับอันที่แล้ว แต่ไม่ค่อยเกี่ยวกับอันแรกนะ

แล้วบอกทำไมมากมาย??? ... นั่นสิ ... ช่างมันดีกว่า เข้าเรื่องเลยละกัน ...

Orthogonal Transformation

คำว่า Orthogonal มันก็แปลว่า ตั้งฉาก อยู่แล้ว ดังนั้น Orthogonal Transformation ก็คือ การแปลงตั้งฉาก ... ???

เอาตัวอย่างมาดูเลยดีกว่า ท่าจะง่ายกว่า

สมมติว่า เดิมเรามีจุด (x, y) = xi + yj อยู่ แล้วเราอยากรู้ว่า ถ้าเปลี่ยนไปเป็นพิกัด au + bv เนี่ย จะได้ค่า a กับ b เป็นเท่าไหร่ เราจะทำยังไง? (เรารู้ค่า u กับ v ในพิกัด i-j อยู่แล้วนะ)

เอารูปเก่ามาดู (จาก ตามหาความหมายของ Determinant: Linear Combination)

วิธีที่เรารู้ ๆ กัน ก็คือใช้กฎของเครเมอร์ หาคำตอบของระบบสมการเชิงเส้น 2 ตัวแปร ก็จะได้ค่า a กับ b ออกมา ดังนี้ (เขียนไว้แล้วใน ตามหาความหมายของ Determinant: Kramer's Rule)

w = (x, y)
a = | w : v | / | u : v |
b = | u : w | / | u : v |
(ถ้าดูเครื่องหมายไม่รู้เรื่อง กลับไปดู ตามหาความหมายของ Determinant: เวกเตอร์ตั้งฉาก ก่อนนะ)

ถ้า u กับ v ตั้งฉากกันหละ? จะมีวิธีหา a กับ b ได้ง่ายกว่านี้รึเปล่า?

ลองดูใหม่นะ เรารู้ว่า

w = au + bv

เอา u ไปคูณ (ภายใน) ทั้งสองข้าง ก็จะได้

u⋅w = u⋅(au + bv)
u⋅w = au⋅u + bu⋅v

จากที่เราสมมติให้ u ตั้งฉากกับ v ดังนั้น u⋅v = 0 สมการก็จะกลายเป็น

u⋅w = au⋅u
a = u⋅w / u⋅u

เอ้อ มันดูง่ายกว่ากฎของเครเมอร์นิดนึงนะ (ตอนนี้อาจจะยังไม่เห็นชัด แต่ว่า พอมันมีหลาย ๆ มิติหนะ จะเห็นชัดมาก)

และแน่นอน ค่า b ก็หาได้ด้วยวิธีเดียวกัน แต่เปลี่ยนจากตอนที่เอา u ไปคูณ (ภายใน) ให้เป็น v แทน สูตรของ b ก็จะเป็น

b = v⋅w / v⋅v

จริง ๆ แล้ว เราขยายข้อสังเกตของเราได้นะ ... สมมติว่า เวกเตอร์แกนใหม่ของเรา มีอยู่ n ตัว คือ v₁ v₂ v₃ ... v_n แล้วเรามีจุด w = (x₁, x₂, x₃, ..., x_n) ใน n มิติอยู่ (ต้องรู้ค่าของเวกเตอร์ทุกตัว ในระบบแกนเดียวกันนะ ไม่งั้นจะหาผลคูณภายในไม่ได้) เราอยากรู้ว่า ในระบบพิกัดของแกนใหม่ ซึ่งระบุด้วย v_i เนี่ย ค่า w_i แต่ละตัวจะหาได้ยังไง? ... กำหนดให้

w = Σ_1≤i≤n w_iv_i

ถ้าหากทุก ๆ v_i ตั้งฉากกันหมด เราจะสามารถหาค่า w_i ทุกตัวได้ด้วยสมการ

w_i = v_i⋅w / v_i⋅v_i

หรือถ้าเขียนรวม ๆ ก็จะเป็น

w = Σ_1≤i≤n (v_i⋅w / v_i⋅v_i) v_i

ซึ่ง ... คราวนี้เห็นชัดเลยหละ ว่ามันง่ายกว่ากฎของเครเมอร์

Orthonormal Transformation

คราวนี้ ถ้าเกิดเรา normalize เวกเตอร์แกนใหม่ทุกตัว ให้เป็น unit vector ก่อนหละ ... มันจะมีอะไรง่ายขึ้นอีก?

คำถามนี้ ตอบง่ายแฮะ ... ก็ดูจากสูตรเมื่อกี๊

w_i = v_i⋅w / v_i⋅v_i

ถ้า v_i ทุกตัว มีขนาดเป็น 1 ... v_i⋅v_i ก็ต้องเท่ากับ 1 ... ดังนั้น

w_i = v_i⋅w
w = Σ_1≤i≤n (v_i⋅w) v_i

Fine ...

ทฤษฎีเซต: Paradox ใน Naive Set Theory

ระบบเซตที่เราใช้ ๆ กันเนี่ย เราเรียกกันว่า Naive Set Theory เพราะมันมีบางอย่างพิเรนทร์อยู่ คิดว่า บางคนคงจะเคยได้ยินชื่อ Russell's Paradox กันมาบ้างแล้ว ... สำหรับใครที่ไม่คุ้น ก็ลองดูนี่ละกัน

Russell's Paradox
ถ้าให้เซต M = { A | A ∉ A } แล้ว M ∈ M หรือ M ∉ M ?

ที่มาของความวุ่นวายนี้ อาจจะเกิดขึ้นเพราะ เซตไม่มีนิยาม ก็ได้

ครั้งนี้ไม่ได้จะเอามาให้ดูแค่ Russell's Paradox หรอกนะ แต่จะบอกว่า มี paradox อีกหลายอัน ที่เกิดจากวลีว่า "เซตของ XXX ทั้งหมด"

ทฤษฎีบทที่สำคัญของ Cantor อันนึง กล่าวไว้ว่า

Cantor's Theorem
สำหรับเซต A ใด ๆ | A | < | 2^A|

เผื่อลืม: 2^A คือ power set ของ A นะ

(นิยามคือ 2^A = { x | x ⊆ A })

วิธีพิสูจน์ ก็ดูได้ที่นี่นะ (มันต้องอาศัยนิยามของ การเปรียบเทียบ cardinal number ด้วย แต่ถือว่า เข้าใจด้วย sense ละกันนะ)

คราวนี้ มาดู paradox อีกอันนึงบ้าง

Set of All Sets (Cantor's Paradox)

ให้ A เป็น เซตของเซตทั้งหมด
จากนิยามของ A และ 2^A ⇒ 2^A ⊆ A ⇒ | A | ≥ | 2^A |
... ขัดแย้งกับ Cantor's Theorem

อีกอัน...

Set of All Cardinal Numbers

ให้ C เป็น เซตของ cardinal number ทั้งหมด
สำหรับแต่ละ i ∈ C ให้ A_i เป็นเซตใด ๆ ที่ | A_i | = i (เลือกมาอันนึง)

ให้ S = ∪_i∈C A_i เราจะรู้ทันทีว่า A_i ⊆ S สำหรับทุก i ∈ C

ที่ i = | 2^S |
จากนิยามของ A_i จะรู้ว่า | A_i | = i = | 2^S |

แต่เนื่องจาก A_i ⊆ S เราจะได้ว่า | A_i | ≤ | S |

ข้อสรุปก็คือ | 2^S | ≤ | S | ... ขัดแย้งกับ Cantor's Theorem

แล้วก็ อีกอันนึง

Set of All Sets Equivalent to a Set

ให้ A เป็นเซตใด ๆ
และ B เป็น เซตของเซตทั้งหมดที่มี cardinal number เท่ากับ | A |

สำหรับทุก i ใด ๆ เราจะรู้ว่า | A | = | A × { i } |
ซึ่งทำให้ A × { i } ∈ B (จากนิยามของ B)
หรือก็คือ { A × { i } }_i∈C ⊆ B สำหรับเซต C ใด ๆ
นอกจากนี้ เรายังรู้แน่ ๆ ว่า | { A × { i } }_i∈C | = | C | ด้วย

พอเราให้ C = 2^B สิ่งที่เกิดขึ้นก็คือ

1. { A × { i } }_i∈C ⊆ B ⇒ | { A × { i } }_i∈C | ≤ | B |
2. | { A × { i } }_i∈C | = | C | = | 2^B |

ก็เลยสรุปได้ว่า | 2^B | ≤ | B | ... ขัดแย้งกับ Cantor's Theorem

แล้ว paradox พวกนี้จะแก้ยังไงหละ? ... ไว้มาต่อกันคราวหน้านะ

อัดมาให้ฟัง - Chopin: Nocturne in C Minor Op. 48 No. 1

ตามชื่อเลยละกัน

Chopin: Nocturne in C Minor Op. 48 No. 1

อัดมาให้ฟัง - Chopin: Polonaise in Ab Major Op. 53

จริง ๆ วันนี้วันที่ 28 น่ะนะ (ขอโกงวันที่หน่อย) เป็นวันแข่งเปียโน แล้วก็...

ตกรอบแรก T_T

จริง ๆ รู้ตัวตั้งแต่ยังอยู่บนเวทีเลย ตอนที่เล่นไปแล้ว 2 เพลง เหลืออีก 2 เพลงอะ รู้แล้วว่าจะเล่นต่อไม่ได้ ... มือมันเย็นเฉียบ แข็งโด๊ก ไม่ขยับเลย T_T

แต่ช่างเถอะ อันนี้ เอามาให้ฟังกันเล่น ๆ นะ เป็นเพลงนึงที่เล่นวันนี้ (วันนี้เล่นไป 4 เพลง เพลงนี้เป็นเพลงสุดท้ายที่เล่น)

ถึงที่อัดมาให้ฟังเนี่ย จะยังไม่ค่อยดี แต่ดีกว่าที่ไปเล่นบนเวทีหลายขุมเลยหละ T_T สถานการณ์การแสดงจริงเนี่ย มันทำให้ฝีมือลดลงได้ เกิน 50% เลยหละ

Chopin: Polonaise in A_b Major Op. 53

อัดมาให้ฟัง - Chopin: Etude Op. 10 No. 10 (Eb Major)

กลัว blog ว่างไป ก็เลยเอาเพลงที่เล่นอัดไว้ตอนซ้อม มาให้ฟังกัน

ต้องขอบอกไว้ก่อนนะ ว่า

1. ยังเล่นไม่ดีเลย
2. ใช้เครื่อง notebook อัดเสียง

ดังนั้น ทั้งคุณภาพเสียง และคุณภาพการเล่น จะอยู่ในเกณฑ์ที่ ค่อนข้างแย่ :P

แล้วดันเอามาให้ฟังอีก ??!!

เอาหนะ ... กลัว blog มันว่างไง :P

Chopin: Etude Op. 10 No. 10 (E^b Major)

เสียงมันเบาด้วยอะ เปิดลำโพงดัง ๆ นะ เวลาฟัง

เอามาให้ฟัง - Scherzo in D Major

เพลงนี้เป็นเพลงที่เคยแต่งไว้ตอนอยู่ ม.4 หนะ (ก็ 7 ปีได้แล้วมั้ง) ไปขุดสมุดเขียนโน้ตเพลงเก่า ๆ แล้วเจอ ก็เลยเอามาให้ดูให้ฟังกัน

(รูปแบบเพลง Scherzo มาจาก Minuet ซึ่ง มีจังหวะเป็น 3/4 และมีท่อน Trio อยู่ตรงกลาง)

ฟัง Scherzo in D Major (.mid)
ดูโน้ต Scherzo in D Major (.pdf)

ไว้มีเวลา จะเอาเพลงอื่น ๆ ที่เคยแต่งไว้ (และที่แต่งใหม่) มาลงให้ดูให้ฟังกันอีกนะ

เอามาให้ฟัง - Short Piece in C Minor

เพลงนี้ เป็นเพลงสั้น ๆ (เด็ก ๆ หน่อย) มีความยาว 20 ห้องเอง

มีโน้ตให้ดูด้วย เอาไปเป็นแบบฝึกหัดเปียโน ระดับพื้นฐานได้นะ :D (ไม่หวง)

ฟัง Short Piece in C Minor (.mid)
ดูโน้ต Short Piece in C Minor (.pdf)

อ้อ แล้วก็ อีกอย่าง ... ไม่รู้จะตั้งชื่อว่าไรดีอะ ... ขอความเห็นหน่อย

Synonym ของคำว่า "โกรธ"

adjective ที่แปลว่า โกรธ โมโห ก็มีดังนี้

• angered (anger [v] = โกรธ | ทำให้โกรธ)
• angry (anger [n] = ความโมโห)
• en'raged (en'rage [v] = ทำให้โมโห)
  
• e'xasperated (e'xasperate [v] = รบกวน, ยั่วโมโห | ทำให้เลวร้าย) = หมดความอดทน
• furious (fury [n])
• in'furiated (in'furiate [v], furious)
• irate/ireful (ire [n] = ความโกรธ ที่อาจจะนำไปสู่ ความมุ่งร้าย)
• livid* = โกรธจัด ๆ | ผิวเปลี่ยนสี (เช่น ซีดเพราะป่วย หรือสีเข้มเพราะช้ำ) | ท่าทางน่ากลัว
• maddened (mad [adj], madden [v])
• pro'voked (pro'voke [v] = ยั่วโมโห | กระตุ้นให้เกิด (เหตุการณ์) | เรียก)
  
• raging (rage [n, v])
• tem'pestuous (tempest [n] = พายุ | ความปั่นป่วน) - คำนี้มักใช้กับปรากฏการณ์ธรรมชาติ แต่ก็ใช้กับคนได้เหมือนกัน
• wild

ต่อด้วย noun ที่แปลว่า ความโกรธ ความโมโห

• anger → anger [v], angry
  
• angriness (angry)
• choler = ความโกรธ | ความขี้รำคาญ
  
• enragement (enrage)
  
• fury → furious
  
• infuri'ation (infuriate)
  
• ire → irate, ireful
  
• li'vidity (livid)
  
• madness (mad)
  
• rage → enrage
  

เค้าจะมีคำพิเศษนิดนึง สำหรับความโกรธที่สมเหตุสมผล (คือ เป็นเพราะ โดนทำอะไรที่ควรจะโกรธหนะ)

• 'incensed [adj] (incense [v] = ทำให้โมโห | ส่งกลิ่นหอมฟุ้งกระจาย)
• in'dignant [adj] → indig'nation [n]
• 'outraged [adj] (outrage [v])
• umbrage [n] → um'brageous [adj]

ความโกรธ + เกลียด (แต่เน้นที่โกรธมากกว่า) ก็จะเป็น

• dander
• hackles - ต้องเติม s นะ ถ้าไม่เติม มันจะเป็นคนละคำ
• huffiness (huffy [adj])
• i'rascibility (i'rascible [adj])
• spleen - อีกความหมายนึงคือ ม้าม นะ

ความโกรธที่เกิดจากความรำคาญ ก็จะมีคำพวกนี้ (ปกติ คำพวกนี้จะมีความหมายอื่นอยู่ด้วยนะ)

• an'noyance (an'noy [v] = สร้างความรำคาญ, รบกวน)
  
• chafe (chafe [v] = annoy | ขัดถูผิวหนัง | เสียดทาน | เอามือมาถูกันให้อุ่น)
• irri'tation ('irritate [v] = รบกวน | กระตุ้น)
  
• ve'xation (vex [v] = annoy | ป่วน | ทำให้งง)
  

adjective ที่มีความหมายว่า โกรธง่าย ขี้โมโห จะเป็นพวกนี้ (ความจุกจิกจู้จี้ ก็รวมอยู่ด้วย)

• bristly (bristle [n, v]) - คำนี้มีอีกความหมาย คือ "ปกคลุมด้วยหนาม"
• choleric (choler [n] = ความโกรธ, ความรำคาญ | อารมณ์ (ที่) เสีย)
• cranky* (crank [n] = คนขี้โมโห, อารมณ์เปลี่ยนเร็ว) = ไม่เสถียร (ใช้กับอะไรก็ได้) | โมโหง่าย
  
• 'hot'headed (hot, head)
• hot-'tempered (temper [n] = อารมณ์)
• huffy → huffiness [n]
• fractious* = ขี้รำคาญ, เจ้าปัญหา
  
• i'rascible* (ire [n], irate [adj])
• irritable (irritate)
• nettlesome (nettle [v]) - จะแปลว่า น่ารำคาญก็ได้นะ (เคยเอามาให้ดูแล้วทีนึง)
• peckish - มีอีกความหมายนึง คือ หิว
  
• peevish* (peeve [v] = ทำให้รำคาญ | ทำให้เกลียด)
• pettish (pet [n] = การแสดงออกถึงความโกรธ)
  
• petulant* → petulance [n]
  
• prickly (prickle [n, v]) = bristly
  
• 'quick-'tempered
• short-'tempered
• sple'netic (spleen [n])
• techy/tetchy
• testy
  
• waspish
• wrathful (wrath)
• wroth
• wrothful (wroth)
  

สุดท้ายละ คำนามต่อไปนี้ หมายถึง การแสดงความโกรธออกมา

• con'niption
• fit
• pet
• scene
• tantrum

เยอะเหมือนกันนะเนี่ย -_-' ...

Synonym ของคำว่า "ความเกลียดชัง" (Noun)

คำว่า "HATE" เนี่ย มันสามารถเป็นได้ทั้ง verb และ noun อยู่แล้ว แต่ส่วนใหญ่เราจะเห็นอีกตัวนึงมากกว่า คือ "HATRED"

คำที่มีความหมายเหมือน ๆ กันกับ hate และ hatred ก็มีประมาณนี้ (noun ทุกตัวนะ)

• ab'horrence (ab'hor)
• abomi'nation (a'bominate) - คำนี้มีอีกความหมาย คือ คนที่น่ารังเกียจ
• an'tipathy (anti-) → antipa'thetic [adj] = ขัดแย้งอย่างรุนแรง
  
• a'version (a'vert [v] = หลีกเลี่ยง, หลบเลี่ยง)
  
• detes'tation (de'test)
• dis'gust (dis'gust [v])
  
• dis'like (dis'like [v])
  
• dis'taste (dis-, taste [n, v])
  
• exe'cration (execrate)
• hate
• hatred
  
• loathing (loath)
• odium → odius [adj]
• re'pugnance (re'pugn [v], re'pugnant [adj]) = aversion ขั้นรุนแรง
  
• re'pulsion (re'pel [v], re'pulse [v]) = repugnance
  
• re'vulsion (ไม่ได้มาจาก revel [v] นะ) = repugnance
• scunner

คาดว่า คงคุ้น ๆ หน้าตาคำพวกนี้อยู่แล้วจากตอนก่อน ๆ (Synonym ของคำว่า "เกลียด" (Verb) กับ Synonym ของคำว่า "น่าเกลียด" และ "น่ารังเกียจ" (Adjective))

แล้วก็ คำที่มีความหมายว่าเกลียดอะไรซักอย่างเป็นพิเศษ มีประมาณนี้ (คำพวกนี้ รวมความมุ่งร้ายอยู่ด้วยนะ)

• mis'anthropy* (mis-, -anthropy) - เกลียดคน
• miso'cainea (mis-) - เกลียดแนวคิดใหม่
  
• mi'sogamy (mis-, -gamy) - เกลียดการแต่งงาน
• mi'sogyny/mi'sogynism (mis-, -gyny) - เกลียดผู้หญิง
• mi'sology (mis-, -logy) - เกลียดการใช้เหตุผล
• miso'neism (mis-) - เกลียดการเปลี่ยนแปลง
• misopedia (mis-) - เกลียดเด็ก
• murderousness (murderous [adj], murder [n, v]) - เกลียดจนอยากฆ่า

เกลียดแบบดูถูก เหยียดหยาม ก็มี... (คำพวกนี้ อาจจะแปลว่า การดูถูก เฉย ๆ ก็ได้นะ)

• con'tempt* (con'temn [v] = ดูถูก เหยียดหยาม)
• de'spisal (de'spise [v] = contemn)
• de'spite (despise) → de'spiteful [adj]
• dis'dain* (dis'dain [v] = contemn | ปฏิเสธด้วยความดูถูก)
• scorn* (scorn [v] = disdain) → scornful [adj]

ส่วนความเกลียดชัง ที่เน้น มุ่งร้าย หนักหน่อย ก็มีดังนี้

• bitterness (bitter [adj])
  
• gall (gall [v] = ทำให้รำคาญ, ทำให้โมโห | ขัดถูจนช้ำ)
  
• rancor/rancour → rancorous [adj] = re'sentful
  
• re'sentment (re'sent)
  

ถ้า มุ่งร้าย หนักมาก จะเป็นพวกนี้

• an'tagonism → an'tagonize [v] = พยายามขัดแย้ง | ยั่วโมโห
• enmity (enemy)
  
• grievance (grieve) - คำนี้ มีความแค้นปนอยู่ด้วย
  
• grudge (grudge [v]) = grievance
  
• hos'tility (hostile [adj])
  
• ill will (ill [adj], will [n])
  
• score = grievance
  

ไว้จะเอาพวกคำที่แปลว่า โกรธ กับ มุ่งร้าย มาให้อีกทีละกัน มันมีอีกเพียบ ... (มันก็เกี่ยวกับความเกลียดชังด้วยแหละ)

Duality: ความเจ๋งของ Abstraction

จริง ๆ เคยแสดงเรื่อง abstraction ให้ดูไปแล้วในเรื่อง แต่คราวนี้อยากจะเอามาพูดถึง เน้นย้ำอีกนิดนึง

ลองดูคุณสมบัติสำหรับตรรกศาสตร์เชิงประพจน์ (Propositional Logic) ข้างล่างนี่ก่อน กฎต่อไปนี้ ใช้กับกรณีที่มีแต่เครื่องหมาย ∧ ∨ กับ ¬ นะ (p q r หมายถึง ประพจน์ใด ๆ หนะ แล้วก็ T หมายถึงเป็นจริง และ F หมายถึงเป็นเท็จ นะ)

1. p ∧ F ≡ F
2. p ∨ T ≡ T
3. p ∧ ¬p = F
4. p ∨ ¬p = T
   
5. ¬(p ∧ q) ≡ ¬p ∨ ¬q
6. ¬(p ∨ q) ≡ ¬p ∧ ¬q
7. p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
8. p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

กฎทั้งหกข้อนี้ เป็นจริงสำหรับพีชคณิต ของตรรกศาสตร์เชิงประพจน์ (แน่นอนสิ) ... แต่เราสามารถทำอะไรได้มากกว่านี้นิดนึงนะ

สมมติว่า เราเปลี่ยนหน้าตาเครื่องหมาย แบบนี้

∧ กลายเป็น ∩
∨ กลายเป็น ∪
T กลายเป็น U
F กลายเป็น ∅
(≡ กลายเป็น =)

เราก็จะได้ กฎสำหรับพีชคณิตของเซต ... ถ้าไปพิสูจน์ดู ก็จะรู้ว่ามันถูก ... แต่อันนี้ ยังไม่เจ๋งหรอก ลองเปลี่ยนอีกแบบดีกว่า

∧ กลายเป็น ∨
∨ กลายเป็น ∧
T กลายเป็น F
F กลายเป็น T

คราวนี้ กฎข้อที่ 1 ของเดิม จะกลายเป็นกฎข้อที่ 2 (ลองกลับขึ้นไปดูสิ) แล้วกฎข้อที่ 2 มันก็กลายเป็นกฎข้อที่ 1 ... !?

อ๊ะ! ... คู่อื่น ๆ (คู่ 3 กับ 4 คู่ 5 กับ 6 แล้วก็คู่ 7 กับ 8) ก็สลับกันเหมือนกัน ... สรุปคือ เราได้กฎเดิม!!! แน่นอนว่า มันก็ต้องถูกสิ เพราะกฎเดิมมันถูก

แล้วมันมีอะไรดีหละ? ... ลองดูอันนี้ละกัน

(p ∨ q) ∧ ¬p ≡ ¬p ∧ q

สมมติไปเลยละกัน ว่าเราพิสูจน์แล้วว่าเป็นจริง (จากกฎทั้ง 8 ข้อข้างบนน่ะแหละ) มันแปลว่า เราสามารถใช้กฎทั้ง 8 ข้อนั้น แปลงรูปฝั่งซ้าย ให้กลายเป็นฝั่งขวาได้

แล้ว ... มันจะเกิดอะไรขึ้น ถ้าเราเปลี่ยนหน้าตาเครื่องหมายแบบที่บอกไว้ ???

(p ∧ q) ∨ ¬p ≡ ¬p ∨ q

อันนี้ก็ต้องถูกต้องด้วยน่ะสิ!!! ... ทำไมน่ะเหรอ?

ก็เพราะว่า ... เราสามารถเลือกใช้กฎ ตามขั้นตอนการพิสูจน์ในแบบแรก (ที่เราสมมติว่า พิสูจน์ได้ไปแล้ว) ได้ในการพิสูจน์ประโยคแบบหลัง (คือ ที่สลับเครื่องหมายแล้วหนะ) น่ะสิ แค่เปลี่ยนจาก ถ้าเดิมใช้ข้อที่ 1 ก็ไปใช้ข้อที่ 2 แทน สลับกันแบบเนี้ย

นี่แหละ ที่เราเรียกว่า Duality ใน Boolean Algebra (มันก็คือ พีชคณิตของตรรกศาสตร์เชิงประพจน์แหละ)

ห้อยท้าย: ถ้าไปนั่งคิดดี ๆ จะเห็นว่า ถ้าเราเขียนวรรค จากรูปแบบปกติประพจน์แยก (Disjunctive Normal Form) โดยให้ แต่ละวรรคมีหน้าตาเป็น A ∧ B ∧ C ∧ ... ∧ Z และเชื่อมกันด้วย ∨ การรวม (Resolution) ก็ยังสามารถทำได้เหมือนกันนะ แต่เค้าไม่นิยมกัน (เท่านั้นเอง)

ตรรกศาสตร์: วรรคฮอร์น และ ภาษา PROLOG

เราจะเรียกวรรควรรคนึงว่าเป็น วรรคฮอร์น (Horn Clause) ก็ต่อเมื่อ มีเพียง predicate เดียวในวรรคนั้น ที่ไม่มีเครื่องหมายนิเสธกำกับ เช่น

¬P(x) ∨ Q(y) ∨ ¬R(z) เป็นวรรคฮอร์น

P(x) ∨ ¬Q(y) ∨ R(z) ไม่เป็นวรรคฮอร์น

ลองสังเกตนิดนึง จะเข้าใจว่า วรรคฮอร์นพิเศษยังไง ...

¬A ∨ ¬B ∨ ¬C ∨ Z
≡ (A ∧ B ∧ C) → Z

ความหมายมันก็คือ การพิสูจน์ว่า Z เป็นจริง สามารถทำได้โดยการ พิสูจน์ว่า A B C เป็นจริงพร้อมกัน

สมมติว่าเรามีวรรคฮอร์นเพิ่มอีกวรรค กลายเป็นสองวรรค ดังนี้

¬A ∨ ¬B ∨ ¬C ∨ Z
¬ D ∨ ¬ E ∨ ¬ F ∨ Z

ถ้าเราต้องการจะพิสูจน์ว่า Z เป็นจริง จะมีทางเลือกให้ 2 ทาง คือ

1. พิสูจน์ว่า A B C เป็นจริงพร้อมกัน
2. พิสูจน์ว่า D E F เป็นจริงพร้อมกัน

ถ้าทำได้ซักทาง ก็แปลว่า Z เป็นจริง แต่ถ้าทำไม่ได้ ก็แปลว่า Z "ไม่จำเป็นต้องจริง" (ไม่ได้แปลว่า ไม่จริง นะ)

วรรคเป้าหมาย (Goal Clause) คือ วรรคที่ predicate ทุกตัว มีเครื่องหมายนิเสธกำกับ เช่น

¬P(x) ∨ ¬Q(y) ∨ ¬R(z)

สมมติว่า เรามีระบบของภาษาอันดับหนึ่ง ซึ่งเมื่อแปลงเป็นรูปแบบวรรคแล้ว ทุกวรรคเป็นวรรคฮอร์น แล้วเราต้องการจะพิสูจน์ว่า วรรคเป้าหมายซักอันนึง เป็นจริงรึเปล่า ... เราต้องพยายามหา วรรคที่รวมกับวรรคเป้าหมายได้

ดูตัวอย่างดีกว่า ถ้าอ่านแล้วงง ... ถ้าเราต้องการจะนิยามประพจน์ Even(x) กับ Odd(x) เมื่อ x เป็นจำนวนเต็มไม่ติดลบ ดังนี้

• Even(x) ≡ x เป็นเลขคู่
• Odd(x) ≡ x เป็นเลขคี่

เราจะรู้ว่า "กฎ" ต่อไปนี้ เป็นจริง

1. Even(0)
2. Even(x) → Odd(NextOf(x))
3. Odd(x) → Even(NextOf(x))

เราก็ แปลงให้เป็นรูปแบบวรรค ได้แบบนี้

1. Even(0)
2. ¬Even(x) ∨ Odd(NextOf(x))
3. ¬Odd(x) ∨ Even(NextOf(x))

วรรคทั้งสามวรรคนี้ เป็นวรรคฮอร์นหมดเลย

สมมติ เราอยากรู้ว่า Odd(NextOf(NextOf(NextOf(0)))) เป็นจริงรึเปล่า (คือ "3 เป็นเลขคี่รึเปล่า" อะนะ) เราก็ต้องตั้งวรรคเป้าหมาย เป็นนิเสธของสิ่งที่ต้องการพิสูจน์ ว่า

Goal: ¬Odd(NextOf(NextOf(NextOf(0))))

เราก็ต้อง พยายามหา predicate ที่รวมกับกฎได้ ... จะเห็นว่า วรรคที่ 2 สามารถรวมกับ วรรคเป้าหมาย ได้ด้วยตัวรวมทั่วไปที่สุด { NextOf(NextOf(0)) / x } ผลลัพธ์ก็จะเป็นวรรคใหม่ อันนี้...

Goal: ¬Even(NextOf(NextOf(0)))

มันก็เป็นวรรคเป้าหมายเหมือนกัน ตามนิยาม ... จะคิดซะว่า เป็นเป้าหมายใหม่ ก็ใช่แหละ ... คราวนี้ วรรคเป้าหมายนี้ ก็สามารถรวมได้กับ วรรคที่ 3 เท่านั้น ตัวรวมทั่วไปที่สุดคือ { Next(0) / x } ผลลัพธ์เป็น วรรคเป้าหมายใหม่อีกวรรค คือ

Goal: ¬Odd(NextOf(0))

หาวรรคมารวมอีกที จะเห็นว่า วรรคที่ 2 เป็นวรรคเดียวที่ใช้ได้ โดยมีตัวรวมทั่วไปที่สุดเป็น { 0 / x } ผลลัพธ์คือ

Goal: ¬Even(0)

คราวนี้ เห็นชัดเลยว่า วรรคที่ 1 จะรวมกับวรรคนี้ได้ และให้ผลลัพธ์เป็นวรรคว่าง ... สรุปว่า 3 เป็นเลขคี่นะ :D

เห็นแล้วใช่มั้ยหละ ว่าวรรคฮอร์น กับวรรคเป้าหมาย มีคุณสมบัติพิเศษคือ

"ผลลัพธ์ของการรวมวรรคฮอร์นกับวรรคเป้าหมาย (เก่า) คือวรรคเป้าหมาย (ใหม่)"

สาเหตุที่วรรคฮอร์น ก่อกำเนิดขึ้น และได้รับความนิยม เป็นเพราะว่า

• ในวรรคเป้าหมาย ทุก predicate ติดนิเสธ
• ในวรรคฮอร์น มี predicate เดียวที่ไม่ติดนิเสธ
• ผลลัพธ์ของการรวม เป็นวรรคเป้าหมาย (ซึ่งทุก predicate ติดนิเสธ)
  

ดังนั้น การค้นหา predicate ที่สามารถรวมกันได้ จะรวดเร็วกว่ากรณีทั่วไป (ที่มีกฎที่ไม่อยู่ในรูปแบบ วรรคฮอร์น)

นอกจากนั้น การเพิ่มข้อกำหนดที่ว่า กฎทุกข้อ ต้องเป็นวรรคฮอร์น ลงไป ทำให้การสร้างโปรแกรมสำหรับช่วยพิสูจน์ ง่ายขึ้นมาก ... มันก็เร็วขึ้นด้วยแหละ อย่างที่บอกไปแล้ว

ภาษา PROLOG

โปรแกรมคอมพิวเตอร์ที่พูดถึงเมื่อกี๊ ก็คือ ภาษา PROLOG น่ะแหละ หน้าตามันจะประมาณนี้

Z :- A, B, C.
Z :- D, E, F.

ความหมายก็คือ ถ้าฝั่งขวาทุกตัวเป็นจริง ฝั่งซ้ายจะเป็นจริง แต่ถ้าจะเขียนว่า ฝั่งซ้ายเป็นจริงเสมอ ก็เขียนได้ โดยไม่ต้องมีเครื่องหมาย ":-" (แต่อย่าลืม "." ลงท้ายนะ) เช่น

Even(0).

ส่วน วรรคเป้าหมาย เค้ามักจะเขียนกันแบบนี้

:- P, Q, R.

ใครสนใจ ลองไปหาตัวแปลภาษา PROLOG เล่นได้ ที่นี่: SWI-Prolog

อ้อ ... สำหรับใครที่เอา SWI-Prolog ไปเล่น ... ชื่อตัวแปรที่ใช้ จะต้องขึ้นต้นด้วยตัวใหญ่นะ นอกนั้น ให้ขึ้นด้วยตัวเล็ก (ทั้งชื่อ predicate ชื่อฟังก์ชัน แล้วก็ชื่อค่าคงที่ด้วย) ... เอาตัวอย่างให้ดูนิดนึง

even(0).
odd(nextof(X)) :- even(X).
even(nextof(X)) :- odd(X).

แล้วก็ ... เค้ามีฟังก์ชันพื้นฐานให้ใช้ เยอะเหมือนกัน จริง ๆ ไม่ต้องเขียน nextof อะไรแบบนี้หรอก ใช้คำสั่ง add เลยก็ได้

Center of Mass & Centroid - Polyhedron

คราวที่แล้ว (เรื่อง Center of Mass & Centroid - Polygon) เราได้แนวคิดการหา centroid ของ polygon แล้ว การขยายเป็น 3 มิติ ก็ทำเหมือน ๆ กันแหละ

การหา centroid ของ polyhedron เราจะใช้แนวคิดจากเรื่อง ต่อจากสูตรเมื่อสมัยเด็ก - ปริมาตรของ Tetrahedron ผนวกกับความจริงที่ว่า

"Centroid ของ Tetrahedron คือ Centroid ของจุดยอดทั้งสี่ของมัน"

ดังนั้น วิธีหา centroid ของ polyhedron ก็คล้าย ๆ กับการหาปริมาตรมันน่ะแหละ เพียงแต่ต้องเอา centroid ของ tetrahedron แต่ละชิ้นเข้าไปคูณด้วย ... สูตรสำเร็จหน้าตาหยั่งงี้

สมมติว่า tetrahedron มีจุดยอดคือ P Q R S

ให้ a = | P : Q : R |
b = | Q : R : S |
c = | R : S : P |
d = | S : P : Q |
C = (a(P + Q + R) + b(Q + R + S) +
c(R + S + P) + d(S + P + Q)) /4(a + b + c + d)

C ก็คือ centroid ของ tetrahedron หนะนะ

คราวนี้ ถ้าเรามี polyhedron ... เราก็สามารถแบ่งมันเป็น tetrahedron หลาย ๆ อันได้ แล้วก็หา centroid ของ tetrahedron เหล่านั้น เอามารวมกันแบบถ่วงน้ำหนักด้วยปริมาตรของมัน แต่การคิดมันจะไม่ง่ายเหมือนกับกรณีของ polygon แล้ว ต้องใช้ความระมัดระวังใน การรวมเข้าหักออก เหมือนกับในการหาปริมาตรของ tetrahedron

แล้วก็ ถึงจะขยายไปเป็นกี่มิติก็ตาม เราก็ใช้หลักการที่ว่า

"Centroid ของ รูปพื้นฐานใน n มิติ ก็คือ Centroid ของจุดยอดทั้งหมด n + 1 จุดของมัน"

แล้วคิดในลักษณะเดียวกัน

Transformation: Domain, Range and Inverse

ย้ำคำเดิมอีกที ... การแปลง (Transformation) มันก็คือฟังก์ชัน (Function) น่ะแหละ ดังนั้น มันต้องมีโดเมนกับเรนจ์ และอาจจะมีอินเวอร์ส

สมมติให้ T เป็นการแปลงที่มีโดเมนเป็น D และเรนจ์เป็น R

เงื่อนไขการมีอินเวอร์สของการแปลง ก็คือ (ทวนของเก่านิดนึงอะนะ)

1. x, y ∈ D → [T(x) = T(y) ↔ x = y]
2. y ∈ R → จะมี x ∈ D ที่ทำให้ T(x) = y
   

ข้อแรก ก็คือที่เราเรียกกันว่า คุณสมบัติหนึ่งต่อหนึ่ง (One-to-One) และข้อสองก็คือที่เรียกว่า คุณสมบัติทั่วถึง (Onto)

เรามักจะเขียนว่า T:A → B เพื่อบอกว่า A เป็นโดเมนของ T และ เรนจ์ของ T เป็นสับเซตของ B นะ

Bijection

สั้น ๆ ก็คือ "ถ้า T เป็น bijection จาก A ไป B แปลว่า T เป็นฟังก์ชันที่มีอินเวอร์ส"

Finite, Infinitely Countable, Uncountable

1. เซต A จะเป็นเซตจำกัด (Finite) ก็ต่อเมื่อ มันมีจำนวนสมาชิกจำกัดไง ... (จะบอกทำไมเนี่ย - -'')
2. เซตจำกัดทุกเซต นับได้ (Countable)
   
3. เซต A จะเป็นเซตไม่จำกัด แต่นับได้ (Infinitely Countable หรือ Countably Infinite) ถ้าสามารถหา Bijection จาก A ไป Z (เซตของจำนวนเต็มหนะ) ได้
4. เซต A จะเป็นเซตนับไม่ได้ (Uncountable) ถ้ามันไม่จำกัด และนับไม่ได้

ความเป็นจริงบางประการ

1. ถ้า A ⊆ Z และ A เป็นเซตไม่จำกัด แล้ว A จะนับได้
2. Q (เซตของจำนวนตรรกยะ) นับได้
   
3. ถ้า A และ B นับได้ A ∪ B กับ A × B จะนับได้
4. R × A จะนับได้ก็ต่อเมื่อ A = ∅
   
5. ช่วง [a, b] (a, b) [a, b) และ (a, b] จะนับไม่ได้ก็ต่อเมื่อ a < b (คือ โดยทั่วไป มันจะนับไม่ได้หนะ)

ตัวอย่าง Bijection ที่ง่าย ๆ (x กับ y เป็นตัวแปร นอกนั้นเป็นค่าคงที่นะ)

• x + a ⇒ (s, t) → (s + a, t + a)
• ax ⇒ (s, t) → (as, at)
• tan x ⇒ (-π/2, π/2) → (-∞, ∞)
• e^x ⇒ (-∞, ∞) → (0, ∞)
• x + y(y + 1)/2 ⇒ (Z⁺ ∪ {0}) × (Z⁺ ∪ {0}) → (Z⁺ ∪ {0})

ตัวอย่าง Bijection ที่พิเรนทร์นิดนึง

ก่อนจะเอาให้ดู ขอตกลงเครื่องหมายนิดนึงก่อน เพื่อให้เขียนง่ายขึ้น

[P] เมื่อ P เป็น predicate จะมีค่าเป็น 1 ถ้า P เป็นจริง และเป็น 0 ถ้า P เป็นเท็จ

เอาหละ ต่อไปนี้คือ bijection ตัวอย่างอีกตัวนึง

• [x ∈ Z] + x ⇒ [0, ∞) → (0, ∞)

bijection แบบนี้ มีได้อีกหลายแบบนะ แต่ที่ต้องการจะสื่อก็คือ ... เราสามารถหา bijection ที่ถ่ายทอดช่วงเปิดไปปิด หรือปิดไปเปิด หรือครึ่งเปิดครึ่งปิด ยังไงก็ได้

Cardinal Numbers

สำหรับเซตนับได้ Cardinal Number ของมันก็คือ จำนวนสมาชิกนั่นเอง ดังนั้น วิธีเขียน cardinal number ของเซต A ก็คือ |A|

คุณสมบัติสำคัญของ cardinal number ก็คือ ถ้าสามารถหา bijection จาก A ไป B ได้ เราจะรู้ว่า |A| = |B|

สำหรับเซตอนันต์ เค้าก็มีการนิยาม cardinal number ไว้เช่นกัน ดังนี้

|Z| = ℵ₀
|R| = c

โดยที่ ℵ₀ คือ cardinal number ที่น้อยที่สุดของเซตอนันต์ (มันเลยห้อย 0 ไง) จะว่าไปก็คือ Z คือเซตอนันต์ที่ "เล็ก" ที่สุดน่ะแหละ

แล้วเค้าก็มีสมมติฐานอันนึง ชื่อว่า Continuum Hypothesis ซึ่งบอกว่า ไม่สามารถหาเซต A ที่ทำให้ ℵ₀ < |A| < c ได้ ... เน้นว่าเป็น สมมติฐาน นะ เพราะว่า มันไม่สามารถพิสูจน์ได้ (ด้วยระบบเซตแบบ Cantor)

คราวนี้ เราอาจจะสรุปบางอย่างได้สะดวกขึ้น เช่น

• ถ้า a < b แล้ว | (a, b) | = | [a, b) | = | (a, b] | = | [a, b] | = c
  
• |2^Z| = 2^ℵ₀ = c
• c² = c × c > c
• ถ้า |A| = ℵ₀ และ 0 < |B| ≤ ℵ₀ แล้ว |A × B| = ℵ₀
• ถ้า |A| = c และ 0 < |B| ≤ ℵ₀ แล้ว |A × B| = c

แถมทิ้งท้าย เปลี่ยนเรื่องนิดนึง

ลองเอาการแปลงที่เคยพูดถึงแล้ว ในเรื่อง Discrete vs Continuous: ฟังก์ชัน เวกเตอร์ และเมตริกซ์ มาดูกันดีกว่า ว่า อันไหนมีโดเมนกับเรนจ์เป็นอะไรบ้าง (ขอละเว้นกรณีจำนวนเชิงซ้อน กับเงื่อนไขบางอย่าง ทิ้งไปก่อนนะ)

• Discrete Fourier Transform
  ⇒D = {f | f:Z_n → R}, R = D
• Fourier Series
  ⇒D = {f | f:[-L, L] → R}, R = {f | f:Z → R}
• Fourier Transformation
  ⇒D = {f | f:R → R}, R = D
• Generating Function
  ⇒D = {f | f:Z⁺ → R}, R = D
• Z Transformation
  ⇒D = {f | f:Z⁺ → R}, R = D
• Laplace Transformation
  ⇒D = {f | f:R⁺ → R}, R = D

หมายเหตุ: D อันนี้ กับ D ในเรื่อง Discrete vs Continuous: ฟังก์ชัน เวกเตอร์ และเมตริกซ์ มันคนละตัวกันนะ

Discrete vs Continuous: สมการผลต่างและสมการอนุพันธ์

หลุดจากหัวข้อนี้ไปนาน ยังไม่ลืมหรอกนะ :D ... ขอโทษอีกทีที่ไม่ได้ update ทุกวันนะ ช่วงนี้ไม่ค่อยมีเวลาได้ต่อเน็ตหนะ

Continuous

เริ่มเลยละกันนะ ... สมมติว่า y เป็นฟังก์ชันของ x ก่อน แล้วก็ มี สมการอนุพันธ์ (Differential Equation) ต่อไปนี้

y' = f(x)

เราก็จะสามารถหา y(x) ได้เท่ากับ

y = ∫_k≤t<x f(t) dt + c

เมื่อ k กับ c เป็นค่าคงที่

Discrete

ในลักษณะเดียวกัน ถ้าเรามี สมการผลต่าง (Difference Equation) ต่อไปนี้

Δy = f(x)

ค่า y(x) ก็จะหาได้จาก

y = Σ_k≤t<x f(t) δt + c

เหมือนกัน

Continuous

คราวนี้ สมมติว่า D = d/dx ... สมการอนุพันธ์ แบบต่อไปที่แก้ง่าย ๆ ก็จะมีหน้าตาประมาณนี้ (เอาดีกรี 2 ก่อนนะ)

D²y + aDy + by = 0

เมื่อ a และ b เป็นค่าคงที่

วิธีแก้สมการนี้ ก็ทำได้ง่าย ๆ โดยการคาดคะเนว่า รูปของคำตอบจะเป็น y = e^mx แล้วแทนค่าลงไป ผลลัพธ์ก็คือ ...

(m² + am + b)y = 0

เนื่องจาก เราไม่ต้องการคำตอบที่ว่า y ≡ 0 ก็เลยเอา y ออกไปได้ กลายเป็นสมการนี้ ...

m² + am + b = 0

สมการพหุนามกำลังสองอันนี้ จะมีคำตอบ m อยู่สองค่า สมมติให้เป็น m₁ กับ m₂ นะ

ถ้า m₁ ≠ m₂ จะได้คำตอบของสมการอนุพันธ์เป็น

y = c₁e^m₁x + c₂e^m₂x

แต่ถ้า m₁ = m₂ จะได้คำตอบเป็น

y = c₁e^m₁x + c₂xe^m₁x

Discrete

ในลักษณะเดียวกัน ถ้าเรามี สมการผลต่าง ต่อไปนี้

Δ²y + aΔy + by = 0

เราจะพยายามเดารูปคำตอบ ที่ทำให้ Δy = my ...

เริ่มจาก

Δa^x = (a - 1) a^x

เราก็สมมติให้ m = a - 1 และ y = (m + 1)^x จะเห็นว่า

y = (m + 1)^x
Δy = m (m + 1)^x = my
Δ²y = m² (m + 1)^x = m²y

คราวนี้ พอแทนค่ากลับลงไปในสมการดั้งเดิม ก็จะได้

m² + am + b = 0

สมการนี้ เหมือนกับในกรณี Continuous เด๊ะเลย (ก็เราจงใจให้มันเป็นงี้หนิ) ถ้าแก้สมการออกมาจะได้ 2 คำตอบ สมมติให้เป็น m₁ กับ m₂ นะ

ถ้า m₁ ≠ m₂ จะได้คำตอบของสมการผลต่างเป็น

y = c₁(m₁ + 1)^x + c₂(m₂ + 1)^x

แต่ถ้า m₁ = m₂ จะได้คำตอบเป็น

y = c₁(m₁ + 1)^x + c₂x(m₁ + 1)^x

Discrete: Recurrence Relation

หลาย ๆ คนคงจะคุ้นเคยกับลำดับ Fibonacci นี่นะ

a_n+2 = a_n+1 + a_n

คราวนี้ ถ้าเราเปลี่ยนหน้าตาตัวแปรซักนิด ให้ n → x แล้วก็ให้ a → y จะเห็นว่า

y(x + 2) = y(x + 1) + y(x)

หรือ ถ้าเขียนใหม่อีกนิดนึงด้วยตัว E จะเป็น

E²y = Ey + y
E²y - Ey - y = 0

หน้าตามันคล้าย ๆ กับสมการผลต่างเลยนะเนี่ย ... งั้น เดี๋ยวเราจะลองแก้สมการนี้เลยดีกว่า

E²y + aEy + by = 0

ถ้าให้ a = b = -1 ก็จะเป็นความสัมพันธ์ Fibonacci นั่นแหละ

คราวที่แล้ว เราเดารูปคำตอบที่ทำให้ Δy = my ... คราวนี้ ลองเดาให้ Ey = my สิ ... ดูมันจะง่ายกว่าเมื่อกี๊อีกนะเนี่ย เพราะว่า

Ea^x = a⋅a^x

ถ้าให้ m = a และ y = a^x เราจะได้ความสัมพันธ์ต่อไปนี้

Ey = my
E²y = m²y

แทนกลับลงไปในสมการตั้งต้น จะได้

m² + am + b = 0

เห็นมาสามรอบละ ... สมมติว่า รากทั้งสองของสมการนี้คือ m₁ กับ m₂ เราก็จะสรุปได้คล้าย ๆ เดิม คือ

ถ้า m₁ ≠ m₂ จะได้คำตอบของสมการดั้งเดิมเป็น

y = c₁m₁^x + c₂m₂^x

แต่ถ้า m₁ = m₂ จะได้คำตอบเป็น

y = c₁m₁^x + c₂xm₁^x

รู้สึกว่า หน้าตามันจะคล้ายกับกรณี continuous มากขึ้นนิดนึงเนอะ

Laplace Transformation

แถมนิดนึงละกัน เพราะว่า Laplace Transformation ก็เป็นเครื่องมืออย่างนึง สำหรับแก้สมการอนุพันธ์

หลักการก็คือ แปลงสมการเริ่มต้นด้วย Laplace Transformation ทีนึง แก้หาคำตอบในโดเมนใหม่ แล้วแปลงกลับด้วย Inverse Laplace Transformation

ตามความนิยม ตัวแปร x ที่เราใช้ ๆ กันเมื่อกี๊ เค้ามักจะเขียนด้วยตัว t แทนนะ เวลาพูดถึง Laplace Transformation หนะ

t domain differential equation
↓ L Transform ↓
s domain polynomial equation
↓ Solving ↓
s domain solution
↓ L^-1 Transform ↓
t domain solution

นิยามของ Laplace Transformation ของฟังก์ชัน f(t) ก็คือ

L[f(t)] = F(s) = ∫_0≤t<∞ f(t) e^-st dt

Z Transformation

Z Transformation ก็คือ Laplace Transformation ในภาคไม่ต่อเนื่องน่ะแหละ มันเอาไว้แก้สมการ E ได้ วิธีทำก็เหมือนกันเลย แต่นิยามต่างกันนิดนึง คือ

Z[f(t)] = F(z) = Σ_0≤t<∞ f(t) z^-t

ที่ใช้ตัว z ก็เพราะความนิยมเหมือนกันอะนะ จริง ๆ จะเขียนเป็น s ก็ได้

Generating Function

ด้วยความนิยมอีกด้านนึง Generating Function ถูกสร้างขึ้นมาจากคนละทิศทางกับ Z Transformation แต่ไป ๆ มา ๆ มันก็คืออันเดียวกันน่ะแหละ แค่มีการเปลี่ยนหน้าตานิดหน่อย คือ

G[f(t)] = F(s) = Σ_0≤t<∞ f(t) s^t

มันต่างกับ z แค่ว่า เลขชี้กำลังของ s มันเป็น +t แต่เลขชี้กำลังของ z มันเป็น -t ซึ่งถ้าให้ s = 1/z มันก็จะเหมือนกันเด๊ะเลย

ดังนั้น วิธีใช้งาน Generating Function กับ Z Transformation ก็เลยเหมือนกันทุกประการ

และ ... แนวคิดนี้ มันก็แนะนำเราว่า ถ้าเราให้ s' = 1/s ใน Laplace Transformation มันก็จะใช้งานได้เหมือนกันนะ

ของนอกอะ... Emergency Chocolate

อันนี้ ของฝากจากออสเตรเลียที่พี่ซื้อมา ...

อ่านฉลากออกป่าวเนี่ย มันเขียนว่า

For immediate relief of: Chocolate Cravings, Lovesickness, Exam Pressure, Mild Anxiety and Extreme Hunger.
Direction for use: Tear open wrapper, break off desired dosage, and consume. Alternatively massage into the affected area. Repeat dosage as required until finished. If symptoms persist consult your local confectioner.

มันมีขายบนเน็ตด้วย http://www.giftboxexpress.com.au/catalogue/category8/c18/p230

Center of Mass & Centroid - Polygon

คราวนี้ จะขยายเรื่องของค่าเฉลี่ยถ่วงน้ำหนักก่อน นิดนึง

เนื่องจาก ผลคูณภายใน มันก็ไม่ได้ห้ามตัวเลขตัวไหนติดลบ ทำไมเราจะใช้ "น้ำหนักติดลบ" ไม่ได้เนอะ

แล้วมันเกี่ยวอะไรกับการหาจุดศูนย์กลางมวลกับ centroid หละ?

เอาตัวอย่างเลยละกัน สมมติเราจะหา centroid ของรูปนี้

เราจะใช้วิธีหาค่าเฉลี่ยถ่วงน้ำหนักได้ง่าย ๆ หยั่งงี้

คำตอบก็คือ

(10 ⋅ (2.5, 4) + 6 ⋅ (4, 1.5)) / (10 + 6) = (25 + 24, 40 + 9) / 16
= (49/16, 49/16)

แต่เราอาจจะใช้อีกวิธีนึง (ทาง Combinatorics เรียกว่า "หลักการการรวมเข้าหักออก" หรือ "Inclusion-Exclusion Principle") ก็คือ น้ำหนักติดลบ แบบนี้

กับ

คำตอบก็คือ

(25 ⋅ (2.5, 2.5) - 9 ⋅ (1.5, 1.5)) / (25 - 9) = (62.5 - 13.5, 62.5 - 13.5) / 16
= (49/16, 49/16)

แล้วหลักการนี้มันใช้ประโยชน์อะไรได้อีก ... ดูชื่อหัวข้อสิ :P

คงต้องบอกอะไรอย่างหนึ่งก่อนนะ คือ ... centroid ของรูปสามเหลี่ยมใด ๆ ก็คือ centroid ของจุดยอดทั้ง 3 ของสามเหลี่ยมนั้น ... ไม่งงนะ ?

คราวนี้ สมมติว่า เราจะหา centroid ของรูปนี้ ซึ่งเรารู้พิกัดของจุดยอดหมดแล้ว (จำรูปนี้ได้ป่าวเอ่ย)

เราก็หา centroid แต่ละชิ้น ถ่วงน้ำหนักด้วยพื้นที่ของมัน (ลองไปดู สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนที่สอง) กับ สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนจบ) นะ ถ้าจำไม่ได้)

หาค่าเฉลี่ยถ่วงน้ำหนัก ก็จะได้ centroid ของรูปที่ต้องการ

สำหรับรูปตัวอย่างนี้ (จริง ๆ คือ รูป 4 เหลี่ยมใด ๆ) ถ้าคิด P Q R S เป็น vector เราจะหา centroid ได้ง่าย ๆ จากสมการต่อไปนี้ (ถ้าจำสัญลักษณ์ | P : Q | ไม่ได้ ลองไปดู ตามหาความหมายของ Determinant: เวกเตอร์ตั้งฉาก นะ)

a = | P : Q |
b = | Q : R |
c = | R : S |
d = | S : P |
C = [a(P + Q) + b(Q + R) + c(R + S) + d(S + P)]
÷ [3(a + b + c + d)]

ข้อสังเกต: พื้นที่ของสามเหลี่ยม คือ | P : Q | / 2 แต่เราเอา / 2 ออกไปได้ เพราะมันจะตัดกันเอง ส่วน centroid ของสามเหลี่ยม คือ (P + Q) / 3

หลักการนี้ จะขยายเป็น polygon กี่จุด มันก็เหมือนกันหนะนะ

ตรรกศาสตร์: Unification

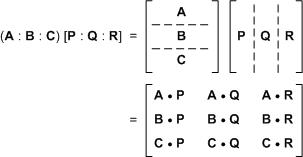
โทษทีนะที่ไม่ได้ update วันต่อวัน ... คือว่า ช่วงนี้ไม่ค่อยมีเวลาอยู่กับเครื่องคอมพิวเตอร์หละ โดนพี่แย่ง :P ขอชดเชย เขียนย้อนหลังไปอีก 2 วันนะ

มาต่อกันเรื่องตรรกศาสตร์อีกนิด จะจบแล้ว ตอนนี้เราทำภาษาอันดับหนึ่ง ให้อยู่ รูปแบบวรรค (Clause Form)

ตัวอย่างที่ 1 สมมติว่าเรามีวรรคต่อไปนี้

¬P(x) ∨ Q(x)
¬Q(y) ∨ R(y)

Q(x) และ ¬Q(y) ในทั้งสองวรรค มันจะรวมกัน (ด้วย Resolution) ได้ถ้า x = y

เนื่องจาก x และ y เป็นตัวแปรที่บ่งปริมาณด้วย ∀ เราจะใช้คุณสมบัติที่ว่า

∀x[P(x)] ∧ ∀y[Q(y)] ≡ ∀x[P(x) ∧ Q(x)]

เพื่อรวมตัวแปรทั้งสองให้เป็นตัวแปรใหม่ตัวเดียว ผลลัพธ์ก็คือ เราจะได้วรรคใหม่ 2 วรรคเป็น

¬P(x) ∨ Q(x)
¬Q(x) ∨ R(x)

คราวนี้ เราจะใช้ Resolution ได้แล้ว ผลลัพธ์ก็คือวรรคใหม่ที่หน้าตาเป็นหยั่งงี้

¬P(x) ∨ R(x)

ข้อสังเกต: วรรค 2 วรรคแรก สามารถแปลงกลับเป็น ∀x[P(x) → Q(x)] กับ ∀x[Q(x) → R(x)] ได้ ส่วนวรรคสุดท้าย ก็สามารถแปลงกลับได้เป็น ∀x[P(x) → R(x)]

ตัวอย่างที่ 2 มาดูเรื่องการเปลี่ยนตัวแปรกัน

สมมติว่ามีวรรคแบบนี้

1. P(x) ∨ ¬Q(x, y) ∨ S(x)
2. R(x, y) ∨ ¬P(y) ∨ S(x)

เราเห็นว่า ตัว P(x) กับ ¬P(y) เนี่ย น่าจะรวมกันได้ เราจะทำแบบเมื่อกี๊ได้มั้ย? ... ถ้าเราเปลี่ยนตัวแปร y ในวรรคที่ 2 ให้เป็น x มันจะกลายเป็น

R(x, x) ∨ ¬P(x) ∨ S(x)

ตัวแปรมันหายไปตัวนึง ... วรรคนี้มันไม่เท่ากับวรรคต้นฉบับแล้ว ... แต่ก็แก้ง่าย ๆ นะ แค่เปลี่ยนเป็นตัวแปรอื่นที่มันไม่ซ้ำกัน ก็ใช้ได้แล้ว (จริง ๆ อันนี้มันก็ใช้ได้แหละ แต่มันไม่ทั่วไปที่สุด ซึ่งเดี๋ยวจะพูดถึง) เอาหละ ลองแทนแบบนี้นะ

• วรรค 1 แทนด้วย { a/x, b/y }
• วรรค 2 แทนด้วย { a/y, c/x } (จริง ๆ เป็น { a/y, b/x } ก็ได้ แต่ผลมันจะไม่เหมือนกัน เดี๋ยวจะทำให้ดูอีกที)

นี่เป็นสัญลักษณ์ที่เค้านิยมใช้กัน หมายถึง การแทนค่า (Substitution) ตัว a/x หมายถึง เอา a ไปแทนที่ x ... ผลลัพธ์ของการแทนค่าก็คือ

3. P(a) ∨ ¬Q(a, b) ∨ S(a)
4. R(c, a) ∨ ¬P(a) ∨ S(c)

มันรวมกันได้แล้ว ผลลัพธ์เป็น

5. ¬Q(a, b) ∨ S(a) ∨ R(c, a) ∨ S(c)

ซึ่งเราจะเปลี่ยนตัวแปรกลับเป็น x y z ก็ได้ เช่น

5. ¬Q(x, y) ∨ S(x) ∨ R(z, x) ∨ S(z)

ตรงนี้เป็นผลลัพธ์ที่ถูกต้องแล้ว แต่เมื่อกี๊บอกไว้นิดนึงว่า จะลองใช้ { a/y, b/x } แทนใน 2 ตอนนี้ทำให้ดูเลยละกัน ว่ามันจะได้อะไร

6. R(b, a) ∨ ¬P(a) ∨ S(b)

แล้วลองดูวรรคที่ 3 อีกที

3. P(a) ∨ ¬Q(a, b) ∨ S(a)

วรรคที่ 6 กับ 3 ก็รวมกันได้ ผลลัพธ์จะเป็น

7. ¬Q(a, b) ∨ S(a) ∨ R(b, a) ∨ S(b)

เอา 5 มามองดู เทียบกับ 7 ดูว่ามันต่างกันยังไง

5. ¬Q(a, b) ∨ S(a) ∨ R(c, a) ∨ S(c)

จะเห็นว่า ถ้าเราแทนค่าด้วย { b/c } ในวรรคที่ 5 เราก็จะได้วรรทึ่ 7 ซึ่งก็แปลว่า 5 เป็น กรณีทั่วไป มากกว่า 7 ดังนั้น ผลลัพธ์การรวมในวรรคที่ 5 จึง น่าจะ ใช้ประโยชน์ได้มากกว่า 7 (เดี๋ยวพูดถึงอีกที)

ตรงนี้ เราได้หลักการหา ตัวรวมทั่วไปที่สุด (Most General Unifier) คร่าว ๆ แล้ว ดังนี้

• มองพจน์ที่ต้องการจะรวม แทนค่าตัวแปรของพจน์นั้นในทั้งสองวรรค ให้พจน์หน้าตาเหมือนกัน
• ตัวแปรอื่น ๆ ที่ยังไม่ถูกแทนค่า (เพราะว่า ไม่ได้อยู่ในพจน์ที่ต้องการจะรวม) ในทั้งสองวรรค ให้แทนค่าเป็น ตัวแปรใหม่ที่หน้าตาไม่เหมือนกัน (ตัวอย่างนี้ คือ a/x ในวรรคที่ 1 และ c/x ในวรรคที่ 2)
  

ตัวอย่างที่ 3 ลองดูอีกอันนึง แบบมีัฟังก์ชันมายุ่งด้วย

1. P(x, f(x)) ∨ R(x)
2. ¬Q(x, f(x), z) ∨ R(x)
3. ¬P(x, y) ∨ Q(x, y, g(x, y)) ∨ ¬R(x)

สมมติว่า เราอยากรวมวรรค 2 กับ 3 ที่ตัว R(x) ด้วยตัวรวมทั่วไปที่สุด ... จะได้

4. ¬Q(x, f(x), z) ∨ ¬P(x, y) ∨ Q(x, y, g(x, y))

แล้วถ้าเพิ่ม { g(x, y)/z, f(x)/y } เข้าไปหละ (y กับ z มันบ่งปริมาณด้วย ∀ เราจะให้มันเป็นอะไรก็ได้) ... เราจะได้อะไรอีกอย่าง

5. ¬Q(x, f(x), g(x, f(x))) ∨ ¬P(x, f(x)) ∨ Q(x, f(x), g(x, f(x)))

ซึ่งมันเท่ากับ

5. ¬P(x, f(x))

รู้สึกว่า วรรคที่ 5 มันจะดูดีกว่า 4 นะ ... หยั่งงี้มันแปลว่า ตัวรวมทั่วไปที่สุดอาจจะไม่ได้ดีที่สุดน่ะสิ ??? (วรรคที่ 4 เกิดจากตัวรวมทั่วไปที่สุด แต่วรรคที่ 5 มันไม่ใช่หนิ)

มันไม่ใช่หยั่งงั้นหรอก :P ลองเอาวรรคที่ 4 รวมกับตัวเองสิ

4. ¬Q(x, f(x), z) ∨ ¬P(x, y) ∨ Q(x, y, g(x, y))

4. ¬Q(x, f(x), z) ∨ ¬P(x, y) ∨ Q(x, y, g(x, y))

คู่เดียวที่จับได้คือ Q(x, y, g(x, y)) กับ ¬Q(x, f(x), z) ดังนั้น ตัวรวมทั่วไปที่สุดก็จะเป็น { g(x, y)/z, f(x)/y } ซึ่งก็คือ ตัวเดียวกับที่เราใช้เพื่อสร้างวรรคที่ 5 ผลลัพธ์ที่ได้ ก็คือวรรคที่ 5 น่ะแหละ

5. ¬P(x, f(x))

คราวนี้ ลองเอาวรรคที่ 1 กับ 5 รวมกัน (ขอเปลี่ยนตัวแปรให้ไม่ซ้ำกันนะ)

1. P(x, f(x)) ∨ R(x)
5. ¬P(y, f(y))

ตัวรวมทั่วไปที่สุดคือ { x/y } (หรือ { y/x }) ได้ผลลัพธ์เป็น

6. R(x)

ข้อสังเกต: เมื่อเราได้วรรคที่ 6 แล้ว วรรคที่ 1 กับ 2 ก็จะไม่มีประโยชน์แล้ว

อีกนิดนึง เรื่องการแทนค่า

เอาตัวอย่างเมื่อกี๊แหละ ตอนที่รวม 2 กับ 3 เข้าด้วยกัน สมมติว่า คราวนี้เราเลือกที่จะรวม Q แทนที่จะรวม R

2. ¬Q(x, f(x), z) ∨ R(x)
3. ¬P(x, y) ∨ Q(x, y, g(x, y)) ∨ ¬R(x)

เราบอกว่า ตัวรวมทั่วไปที่สุดคือ { g(x, y)/z, f(x)/y } ... ลองเอาไปแทนค่า จากซ้ายไปขวา

Q(x, f(x), z) ⋅ { g(x, y)/z } = Q(x, f(x), g(x, y))
Q(x, f(x), g(x, y)) ⋅ { f(x)/y } = Q(x, f(x), g(x, f(x)))

แล้วถ้าเราแทนจากขวาไปซ้ายหละ?

Q(x, f(x), z) ⋅ { f(x)/y } = Q(x, f(x), z)
Q(x, f(x), z) ⋅ { g(x, y)/z } = Q(x, f(x), g(x, y))

มันไม่เหมือนกัน!!! ถ้าแทนจากซ้ายไปขวา จะไม่มีตัว y เหลือ แต่พอแทนจากขวาไปซ้าย มันดันมีตัว y เหลืออยู่...

มันก็แปลว่า ตอนที่เราหาตัวรวมทั่วไปที่สุด เราต้องหาลำดับที่ถูกต้องเลยรึเปล่า?

จริง ๆ แล้วไม่ต้องหรอก แต่ตอนหาต้องระวังนิดนึง ... มันมี algorithm อยู่ ดูนี่นะ

Q(x, f(x), z)
Q(x, y, g(x, y))

เริ่มต้น เราก็ดูว่า parameter แรก มันรวมกันได้รึเปล่า ... มันเป็น x กับ x อยู่แล้ว ไม่ต้องสน ดูตัวต่อไปเลย

Q(x, f(x), z)
Q(x, y, g(x, y))

คราวนี้ f(x) กับ y มันจะรวมได้ถ้าเราใช้ { f(x)/y } (ตัวที่ถูกแทนที่ ต้องเป็นตัวแปรเสมอนะ) คราวนี้ เราจะดูตัวต่อไป

Q(x, f(x), z)
Q(x, y, g(x, y))

ตรงนี้แหละที่มันแปลก ๆ เพราะว่าเมื่อกี๊เรากำจัดตัว y ไปแล้ว ทำไมมันยังมีอยู่? ... จริง ๆ แล้วเราต้องเอา { f(x)/y } เมื่อกี๊ ไปแทนในโจทย์เลยต่างหาก มันจะเป็น

Q(x, f(x), z)
Q(x, y, g(x, f(x)))

นี่สิ ถึงจะถูก!! ... ทำต่อนะ ตัวรวม z กับ g(x, f(x)) ก็คือ { g(x, f(x))/z }

ตัวรวมทั่วไป ก็คือ { f(x)/y, g(x, f(x))/z } นั่นเอง ... แต่มันไม่ตรงกับ คราวที่แล้วนะ คราวที่แล้วมันเป็น { g(x, y)/z, f(x)/y } ?

มันก็ไม่ตรงแหละ แต่เวลาเอาไปแทนค่า มันจะได้ผลลัพธ์เหมือนกัน (ไม่เชื่อก็ลองสิ :P)

หมายเหตุ: algorithm การหาตัวรวมทั่วไปที่บอกเนี่ย มันมอง parameter จากซ้ายไปขวา ผลลัพธ์ก็เป็น { f(x)/y, g(x, f(x))/z } แต่ลำดับการมอง parameter จริง ๆ แล้ว มันจะเป็นยังไงก็ได้ ถ้ามองจากขวาไปซ้าย ก็จะได้ตัวรวมทั่วไปที่บอกไว้ตอนแรก คือ { g(x, y)/z, f(x)/y } ตัวรวมที่ได้ อาจจะไม่เหมือนกัน แต่พอเอาไปแทนค่า มันจะเหมือนกัน

การพิสูจน์แบบ Resolution-Refutation สำหรับภาษาอันดับหนึ่ง

เมื่อกี๊เรารู้แล้ว ว่า Resolution สามารถทำกับวรรคได้ยังไง เราก็ใช้หลักการเดียวกับที่เคยบอกไว้ใน ตรรกศาสตร์: รูปแบบปกติประพจน์รวม ได้ ซึ่งก็คือ

1. ใส่นิเสธที่ประพจน์ที่ต้องการพิสูจน์
2. แปลงประพจน์ทั้งหมด (ทั้งที่กำหนดให้ และที่ต้องการพิสูจน์) ให้อยู่ในรูปแบบวรรค
3. ทำ Resolution จนกว่าจะได้ประพจน์ว่าง

แต่กรณีของภาษาอันดับหนึ่งเนี่ย มันต่างไปตรงที่ ... มันสามารถทำ resolution ได้เรื่อย ๆ ไม่สิ้นสุดน่ะสิ

ดังนั้น ถ้าประพจน์ที่ต้องการพิสูจน์เป็นจริง เมื่อได้ประพจน์ว่างเราก็จะรู้ แต่ถ้ามันไม่จริง เราก็อาจจะต้องทำไปเรื่อย ๆ เรื่อย ๆ ... เหมือนกับ ไม่มีทางรู้เลย ว่ามันเป็นจริงรึเปล่า

จะว่าไป มันก็เทียบได้กับ halting problem น่ะแหละ (เทียบได้จริง ๆ นะ เหมือนกัันเด๊ะเลย)

เฮ่อ ... จบแล้ว เรื่อง algorithm ของภาษาอันดับหนึ่ง คราวหน้าเรื่อง วรรคฮอร์น (Horn Clause) และ ภาษา PROLOG นะ

Paradox ... รึเปล่า?

ช่วงนี้ อยู่ในเทศกาลกินเจ บ้านผมก็กินเจกันเกือบทุกคนครับ (คือ อย่างน้อย ก็แม่ กับผม) วันนี้ไปช็อปที่ Marketplace แล้วแม่ผมก็ซื้ออาหารเจ และวัตถุดิบสำหรับทำอาหารเจมา

แต่สิ่งที่ไม่ใช่อาหารที่ซื้อมา มันมีไอ้นี่อยู่ด้วย...

... :P

เจปัง

ไปเจอเจปังของจริงมาแล้ว ...

มันไม่มีส่วนผสมของวัตถุดิบที่มาจากสัตว์หนะ

Center of Mass & Centroid - บทแรก

วันนี้จะพูดถึง วิธีหา จุดศูนย์กลางมวล (Center of Mass) ... คิดว่าคงรู้จักกันอยู่แล้วนะว่ามันคืออะไร

ก่อนอื่น คิดว่าตอนเด็ก ๆ หลาย ๆ คนคงเคยเอากระดาษมาตัดเป็นรูป แล้วยึดจุดนึง ปล่อยมันห้อย ลากเส้นตามแนวดิ่งจากจุดยึด จากนั้นก็เปลี่ยนจุดแล้วทำซ้ำไปเรื่อย ๆ จุดตัดของเส้นที่ลากหลาย ๆ เส้นเนี่ย มันก็จะเป็นจุด CM

แล้ววิธีคิดแบบที่ไม่ต้องไปห้อย ๆ เอาหละ ทำยังไง? สมมติเรารู้รูปร่างและตำแหน่งของวัตถุ แล้วเราจะหาจุดศูนย์กลางมวลมันได้มั้ย?

คำตอบก็คือ ... ไม่ได้ ครับ นอกจากเราจะกำหนด ความหนาแน่นของมวลต่อตำแหน่ง ซะก่อน ...

แล้วถ้าเรารู้แล้วหละ ... เราจะหามันได้ยังไง?

เริ่มจาก ... วัตถุที่เป็นจุด ๆ ก่อน ... สมมติว่าเรามีวัตถุอยู่ n ก้อน แต่ละอันมีมวล w_i และอยู่ที่ตำแหน่ง r_i (1 ≤ i ≤ n) เราก็จะรู้ว่า ... (จาก Discrete: ผลคูณภายใน และ การถ่วงน้ำหนัก)

r_cm = R ⋅ w / α ⋅ w
เมื่อ w = (w₁, w₂, w₃, ..., w_n)
R = (r₁, r₂, r₃, ..., r_n)
และ α = (1, 1, 1, ..., 1)

r_cm ที่ได้เนี่ย ก็คือ ตำแหน่งของจุดศูนย์กลางมวล ของกลุ่มวัตถุ นั่นเอง

ถ้าเราเขียนเวกเตอร์ในรูปของฟังก์ชันแทน ... สมมติให้โดเมนเป็น S ก็จะได้ว่า

r_cm = R ⋅ w / α ⋅ w
เมื่อ w(x) = มวลของวัตถุก้อนที่ x
R(x) = ตำแหน่งของวัตถุก้อนที่ x
และ α(x) = 1
สำหรับทุก x ∈ S

นี่มันก็สูตรค่าเฉลี่ยธรรมดา ๆ แหละ :P ... แต่จริง ๆ มันพิเศษกว่านี้ได้นิดนึงนะ เพราะว่า ถ้า a ≠ b แล้ว เราจะรู้ว่า R(a) ≠ R(b) เราก็เลยสามารถเขียนใหม่ ให้มันหด ๆ ลงหน่อย ได้เป็น ... (ถ้าสงสัย ก็ถามมาใน comment ด้วยนะ)

r_cm = x ⋅ w / α ⋅ w
เมื่อ w(x) = มวลของวัตถุที่ตำแหน่ง x
และ α(x) = 1
สำหรับทุก x ∈ S

ถ้าวัตถุของเราทุกชิ้น มีมวลเท่ากันหมด ซึ่งก็แปลว่า w(x) = 1 (หรือก็คือ w = α) เราจะเรียกจุดศูนย์กลางนี้ว่า Centroid สูตรก็คือ

r_centroid = x ⋅ α / α ⋅ α
เมื่อ α(x) = 1
สำหรับทุก x ∈ S

สรุปสูตรแบ่งเป็นกรณี discrete กับ continuous นะ...

กรณี Discrete

ให้ S เป็นเซ็ตของจุดที่มีวัตถุอยู่
และ w(x) คือมวลของวัตถุที่จุด x

กรณี Continuous

ให้ S เป็นเซ็ตของจุดที่มีวัตถุอยู่
และ w(x) dS คือมวลของวัตถุที่จุด x

ทั้งสองสูตรนี้ เป็นสูตรที่เห็นได้ตามหนังสือทั่วไปเลยหละ

คราวหน้าจะมาดูกรณี polygon เป็นพิเศษนะ ... มันจะไปผูกกับ determinant นิดหน่อย

แนะแนว GRE General Test นิดนึง

ผมเคยสอบ GRE ไปแล้ว แล้วก็คิดว่า มีหลาย ๆ อย่างที่น่าจะเป็นประโยชน์กับเพื่อน ๆ ที่อยากจะสอบ GRE ได้

ข้อมูลละเอียด สามารถไปดูได้ที่ http://www.gre.org/ นะ

ข้อมูลต่อไปนี้ มีกลุ่มเป้าหมายหลักคือ คนที่เรียนจบสาขาที่ต้องใช้เลขนะ คนอื่น ๆ ก็อ่านได้แต่อาจจะเป็นอันตรายนิดหน่อย :P แล้วก็ คนที่เก่งภาษาอังกฤษอยู่แล้ว อาจจะรู้สึกว่า มันไม่น่าจะยากขนาดนั้นนี่นา 555

ข้อสอบ GRE เนี่ย แบ่งเป็น 2 แบบ คือ General Test กับ Subject Test วันนี้จะพูดถึงแต่ General Test นะ

ข้อสอบ GRE General Test จะแบ่งเป็น 3 ส่วน คือ

1. Quantitative (เต็ม 800) - เลข
2. Verbal (เต็ม 800) - คำศัพท์
3. Analytical Writing (เต็ม 6) - ชื่อบอกอยู่แล้วอะ

ส่วน Quantitative ไม่พูดถึงนะ ถ้าได้ไม่เต็มก็เกือบเต็ม มาเจาะเรื่อง Verbal กันก่อน

Verbal

ข้อสอบ Verbal เป็น Choice ที่มี 5 ตัวเลือกนะ โจทย์จะมี 30 ข้อ ซึ่งแบ่งเป็น 4 แบบ คือ

1. Sentence Completion
2. Reading Comprehension
3. Analogy
4. Antonym

โจทย์แต่ละแบบ มันจะมาสลับกันเรื่อย ๆ (คือ ไม่ได้เรียงเป็น Sentence Completion หมดก่อนแล้วค่อย Reading Comprehension อะไรเงี้ย) มาเจาะลึกกันดีกว่า ว่าแต่ละแบบมันเป็นไง

Sentence Completion

ชื่อค่อนข้างบ่งบอกนะว่าเป็นยังไง มันจะมีประโยคมาให้ แล้วก็มีช่องว่าง ให้เลือกเติมให้เหมาะสมหนะ โจทย์แบบนี้ (Sentence Completion อะ) ถือว่าง่ายที่สุดใน Verbal แล้ว เพราะเดาได้ มีข้อมูลให้เยอะสุด

ตัวอย่างเช่น (เอามาจาก Kaplan นะ ... แอบผิดกฎหมายนิดนึง :P)

Despite much informed ____, the relationship between sunspot cycles and the earth's weather remains ____.
A) argument . . . decisive
B) confusion . . . tenuous
C) conjecture . . . ambiguous
D) evidence . . . clear
E) analysis . . . systematic

ก็ ... ถ้าเราแปลออกทุกตัว มันก็คงไม่ยากหรอกเนอะ :D แต่จริง ๆ ไม่ต้องแปลออกหมดก็ตอบได้นะ choice เค้าค่อนข้างดี คือ ถ้าเจออันไหนฟังเข้าท่า ก็ไม่ต้องไปดูตัวอื่นหละ มันถูกแน่ ๆ (อันนี้ตอบข้อซีนะ)

Reading Comprehension

เป็นเรื่องที่ไม่น่าเชื่อ แต่ว่า Reading Comprehension นี่ยากมากเลย ไม่หมูเหมือน TOEFL นะ แถมยังกินเวลามาก ๆ ด้วย เพราะถ้าโชคร้าย อาจจะต้องอ่านอะไรที่ยาวประมาณ 100 บรรทัดแคบ ๆ (ใครเคยสอบ TOEFL คงรู้แล้วว่าบรรทัดมันแคบ)

ข้อแนะนำสำหรับ part นี้ มีไม่มาก คือ พยายามทำเวลาหน่อย ในข้อสอบ Verbal จะมี Reading Comprehension ประมาณ 2-3 (มักจะเป็น 3) ชุด แต่ละชุดก็จะมีคำถาม 2-4 ข้อ ในห้องสอบมันจะมีนาฬิกาให้ดู ว่าเหลือกี่นาที ต้องลองคำนวณดูด้วยนะ ว่าทำช้าไปรึเปล่า

เพื่อให้คุ้นกับความยากของมัน ลองไปโหลดข้อสอบตัวอย่างมาดูสิ (เดี๋ยวเอา link ให้)

Analogy

โจทย์ Analogy เป็นคำศัพท์ล้วน ๆ เลย คงไม่ต้องอธิบายมากละกัน เอาโจทย์ให้ดูเลย (ผิดกฎหมายอีกแล้ว)

EXTORT : OBTAIN
A) plagiarize : borrow
B) pilfer : steal
C) explode : ignite
D) purify : strain
E) consider : appeal

choice มันก็จะดีเหมือนกันนะ คือ ไม่ (ค่อย) คลุมเครือ แบบว่า ถ้าเราเลือก "ความสัมพันธ์" ระหว่างคำถูก พอเอาไป "เสียบ" กับ choice มันจะได้ choice เดียว แล้วก็ ไม่มีแบบคิดลึกนะ พยายามอย่าคิดเกิน ต้องใช้ sense ด้วยนิดนึง (โจทย์ข้อนี้ ตอบข้อแรกนะ)

Antonym

Antonym มันก็แปลว่า คำศัพท์ที่มีความหมายตรงข้ามกัน อยู่แล้ว เอาตัวอย่างไปดู ...

VIVACITY:
A) animosity
B) efficacy
C) torpor
D) subtlety
E) tedium

โจทย์ Antonym นี่ โหดสุดเลย วัดความจำแท้ ๆ ... ไม่มีคำแนะนำอะไรนอกจาก ท่องศัพท์ไปเยอะ ๆ นะ (ข้อตัวอย่างนี่ ตอบข้อซีนะ)

Analytical Writing

ในการสอบ GRE นี่ ต้องเขียน 2 อันนะ คือ

1. Issue Writing - 45 นาที
2. Argument - 30 นาที

Issue Writing

อันนี้คล้าย ๆ กับโต้วาทีอะ คือ เค้าจะมีญัตติมาให้ แล้วเราจะเลือกเป็นฝ่ายเสนอ หรือฝ่ายค้าน วิธีเขียน ก็เหมือนกับใน TOEFL แหละ คือ เขียน ๆ ไปเถอะ แต่ใน GRE เค้าจะเน้นที่ความหมายมากกว่า Grammar ก็ใน GRE มันเรียกว่า Analytical Writing นี่นา

ตัวอย่างหัวข้อ ก็เช่น

"It is possible to pass laws that control or place limits on people's behavior, but legislation cannot reform human nature. Laws cannot change what is in people's hearts and minds."

สังเกตว่า มันมี 2 ประโยค เราจะเห็นด้วยหรือไม่เห็นด้วยแยกประโยคกันก็ได้ เช่น เราจะเห็นด้วยกับประโยคแรก แต่ไม่เห็นด้วยกับประโยคที่สอง ก็ได้ แต่ที่สำคัญที่สุดคือ ต้องให้เหตุผลที่ฟังดูดี และ (เหมือนจะ) สมเหตุสมผล

วิธี organize โดยทั่วไป ก็เหมือน TOEFL คือ

• ย่อหน้าแรก - เป็นบทนำ ควรจะบอกให้ชัดเจนไปเลยว่า เราเห็นด้วยหรือไม่เห็นด้วย แล้วอาจจะมี outline ว่าย่อหน้าต่อ ๆ ไปจะเกี่ยวกับอะไร (จะไม่มีก็ได้นะ)
• ย่อหน้าต่อ ๆ ไป ประมาณ 2-4 ย่อหน้า - เป็นเหตุผลสนับสนุนความคิดเรา ควรจะมี 1 main idea ต่อย่อหน้า และ topic sentence ควรจะเป็นประโยคแรกหรือสุดท้าย (ไม่จำเป็นนะ แค่ "ควร") จริง ๆ จะเขียนเกิน 4 ก็ได้นะ ถ้ามีแรงพอ
  
• ย่อหน้าสุดท้าย - เป็นสรุป ก็เหมือนพูดซ้ำอีกที ว่าทำไมเราถึงคิดอย่างที่เขียนไปในบทนำ

ตัวอย่างหัวข้อที่ ETS จัดให้ ไปดูได้ที่นี่นะ The Pool of Issue Topics เค้าบอกว่า จะออกสอบจากในนี้แหละ แต่อาจจะไม่เหมือนเด๊ะ

Argument Writing

อันนี้จะต่างกัน Writing ของ TOEFL ลิบลับเลย โจทย์มันคือ เค้าจะมีให้อ่านสั้น ๆ แล้วให้เราให้ความเห็นถึง วิธีการใช้เหตุผล ของผู้เขียน (หรือผู้พูด) เช่น

"Twenty years ago, one half of all citizens in Corpora met the standards for adequate physical fitness as then defined by the national advisory board on physical fitness. Today, the board says that only one quarter of all citizens are adequately fit and suggests that spending too much time using computers may be the reason. But since overall fitness levels are highest in regions of Corpora where levels of computer ownership are also highest, it is clear that using computers has not made citizens less physically fit. Instead, as shown by this year's unusually low expenditures on fitness-related products and services, the recent decline in the economy is most likely the cause, and fitness levels will improve when the economy does."

อ่าน ๆ ดูจะเห็นว่า มันมีบางอย่างไม่สมเหตุสมผลอยู่ ... เราก็ต้องเขียนเพื่อบอกว่า ตรงไหนไม่สมเหตุสมผล เช่น ยกตัวอย่างที่สอดคล้องกับ "หลักฐาน" แต่ขัดแยังกับ "ข้อสรุป" และถ้าเป็นไปได้ ก็แนะนำว่า ควรจะแก้ยังไงให้ดี

วิธี organize ก็เหมือนกัน แต่อันนี้จะง่ายกว่านิดนึงตรงที่ บทนำ กับ สรุป เนี่ย สามารถซ้อมไปได้ เพราะมันค่อนข้างจะไม่ขึ้นกับโจทย์

ส่วนเนื้อหาเนี่ย จะเกิดจากการ "จับผิด" เค้า เราจับผิดได้กี่จุด ก็จะมีจำนวนย่อหน้าเท่านั้น + 2 แต่ถ้าเราจับผิดได้มากเกินไป ก็เลือกเอาเฉพาะจุดที่สำคัญที่สุดมา ซัก 2-4 จุด ก็พอ

• ย่อหน้าแรก - บทนำ ควรจะบอกว่า ที่เค้าเขียนมาเนี่ย มันยังไม่สมบูรณ์ (หรือเชื่อถือไม่ได้น่ะแหละ) เพราะว่า ใช้เหตุผลไม่ถูกต้อง หรืออะไรประมาณเนี้ย
• ย่อหน้าต่อ ๆ ไปประมาณ 2-4 ย่อหน้า - ควรจะอธิบายจุดที่ผิดพลาด 1 จุด ต่อ 1 ย่อหน้า โดยขยายความ คล้าย ๆ ว่า ยกตัวอย่างที่สอดคล้องกับหลักฐาน แต่ขัดแย้งกับข้อสรุป อาจจะใช้วิธีสมมติหลักฐานใหม่ ที่ไม่ขัดแย้งกับหลักฐานเดิม แล้วทำให้เกิดข้อขัดแย้งกับบทสรุปก็ได้ แล้วก็ถ้าเป็นไปได้ ควรจะบอกด้วยว่า ข้อผิดพลาดนี้ น่าจะแก้ได้ด้วยวิธีอะไร
• ย่อหน้าสุดท้าย - สรุป เนี่ย ท่องได้เลย ความหมายควรจะประมาณว่า ... In sum, if all the flaws are fixed as described, this argument will become logically valid. แต่อาจจะเขียนยาวกว่านี้ เช่น ย้ำอีกทีว่า flaw มันมีอะไรบ้าง หรือ ควรจะแก้อะไรบ้าง

ตัวอย่าง Argument ที่ ETS จัดให้ ไปดูได้ที่นี่นา The Pool of Argument Topics

Link จ้า

สมัครแบบ on-line ได้เลยที่ http://www.gre.org/ นะ
แล้วก็ โปรแกรมเตรียมสอบ (จริง ๆ ก็ไปโหลดได้จากใน http://www.gre.org/ น่ะแหละ)

---

สรุปคำศัพท์

animosity [n] = ความเป็นศัตรู → animus [n] = animosity
extort [v] = รีดไถ → extortion [n]
pilfer [v] = จิ๊ก, ขโมย (เล็ก ๆ น้อย ๆ) → pilferage [n]
plagiarize [v] = ขโมยคำพูด/งานเขียน/ทรัพย์สินทางปัญญา
subtle [adj] = เ้ข้าใจยาก | เก่ง | เจ๋ง → subtlety [n]
tedium [n] = ความน่าเบื่อ, ความน่าเหนื่อยหน่าย → tedious [adj]
tenuous [adj] = (ปริมาณ) น้อย | เล็กน้อย, ไม่สำคัญ → tenuity [n]
torpor [n] = ความเฉื่อยชา → torpid [adj]
vivacity [n] = ชีวิตชีวา → vivacious [adj]