Center of Mass & Centroid - บทแรก

วันนี้จะพูดถึง วิธีหา จุดศูนย์กลางมวล (Center of Mass) ... คิดว่าคงรู้จักกันอยู่แล้วนะว่ามันคืออะไร

ก่อนอื่น คิดว่าตอนเด็ก ๆ หลาย ๆ คนคงเคยเอากระดาษมาตัดเป็นรูป แล้วยึดจุดนึง ปล่อยมันห้อย ลากเส้นตามแนวดิ่งจากจุดยึด จากนั้นก็เปลี่ยนจุดแล้วทำซ้ำไปเรื่อย ๆ จุดตัดของเส้นที่ลากหลาย ๆ เส้นเนี่ย มันก็จะเป็นจุด CM

แล้ววิธีคิดแบบที่ไม่ต้องไปห้อย ๆ เอาหละ ทำยังไง? สมมติเรารู้รูปร่างและตำแหน่งของวัตถุ แล้วเราจะหาจุดศูนย์กลางมวลมันได้มั้ย?

คำตอบก็คือ ... ไม่ได้ ครับ นอกจากเราจะกำหนด ความหนาแน่นของมวลต่อตำแหน่ง ซะก่อน ...

แล้วถ้าเรารู้แล้วหละ ... เราจะหามันได้ยังไง?

เริ่มจาก ... วัตถุที่เป็นจุด ๆ ก่อน ... สมมติว่าเรามีวัตถุอยู่ n ก้อน แต่ละอันมีมวล w_i และอยู่ที่ตำแหน่ง r_i (1 ≤ i ≤ n) เราก็จะรู้ว่า ... (จาก Discrete: ผลคูณภายใน และ การถ่วงน้ำหนัก)

r_cm = R ⋅ w / α ⋅ w
เมื่อ w = (w₁, w₂, w₃, ..., w_n)
R = (r₁, r₂, r₃, ..., r_n)
และ α = (1, 1, 1, ..., 1)

r_cm ที่ได้เนี่ย ก็คือ ตำแหน่งของจุดศูนย์กลางมวล ของกลุ่มวัตถุ นั่นเอง

ถ้าเราเขียนเวกเตอร์ในรูปของฟังก์ชันแทน ... สมมติให้โดเมนเป็น S ก็จะได้ว่า

r_cm = R ⋅ w / α ⋅ w
เมื่อ w(x) = มวลของวัตถุก้อนที่ x
R(x) = ตำแหน่งของวัตถุก้อนที่ x
และ α(x) = 1
สำหรับทุก x ∈ S

นี่มันก็สูตรค่าเฉลี่ยธรรมดา ๆ แหละ :P ... แต่จริง ๆ มันพิเศษกว่านี้ได้นิดนึงนะ เพราะว่า ถ้า a ≠ b แล้ว เราจะรู้ว่า R(a) ≠ R(b) เราก็เลยสามารถเขียนใหม่ ให้มันหด ๆ ลงหน่อย ได้เป็น ... (ถ้าสงสัย ก็ถามมาใน comment ด้วยนะ)

r_cm = x ⋅ w / α ⋅ w
เมื่อ w(x) = มวลของวัตถุที่ตำแหน่ง x
และ α(x) = 1
สำหรับทุก x ∈ S

ถ้าวัตถุของเราทุกชิ้น มีมวลเท่ากันหมด ซึ่งก็แปลว่า w(x) = 1 (หรือก็คือ w = α) เราจะเรียกจุดศูนย์กลางนี้ว่า Centroid สูตรก็คือ

r_centroid = x ⋅ α / α ⋅ α
เมื่อ α(x) = 1
สำหรับทุก x ∈ S

สรุปสูตรแบ่งเป็นกรณี discrete กับ continuous นะ...

กรณี Discrete

ให้ S เป็นเซ็ตของจุดที่มีวัตถุอยู่
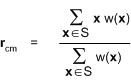
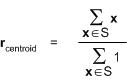
และ w(x) คือมวลของวัตถุที่จุด x

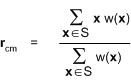
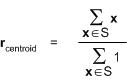
กรณี Continuous

ให้ S เป็นเซ็ตของจุดที่มีวัตถุอยู่
และ w(x) dS คือมวลของวัตถุที่จุด x

ทั้งสองสูตรนี้ เป็นสูตรที่เห็นได้ตามหนังสือทั่วไปเลยหละ

คราวหน้าจะมาดูกรณี polygon เป็นพิเศษนะ ... มันจะไปผูกกับ determinant นิดหน่อย