ถึงคราวต้องสร้าง Virtual Machine แล้ว (พื้นฐาน)

เพื่อให้เห็นภาพ ว่าที่ผ่าน ๆ มา มันเป็นอะไร คราวนี้ มาลองสร้าง Virtual Machine กันเถอะ ... มาสรุปสิ่งที่ Virtual Machine ควรจะมีก่อน ... ครั้งนี้คิดสำหรับ process เดียวก่อนนะ

Memory Units

เพื่อให้สามารถสร้าง memory module ได้ เราต้องกำหนดไว้ก่อนว่า แต่ละ word มีขนาดเท่าไหร่ ... สมมติเลยละกันนะ ว่า

ตำแหน่งของ memory 1 ตำแหน่ง จะเก็บข้อมูลได้ 1 byte
ขนาดของ instruction = 4 byte

Process Space

• PC - Program Counter
  
• Memory - แบ่งเป็น
  
• Stack
• SP - Stack Pointer
• BP - Base Pointer
  
• Heap
  
• MA - Memory Address
  
• AC - Accumulator
• FP - Frame Pointer

และ operation ที่เกี่ยวกับ memory พื้นฐาน ก็คือ

• load: AC ← mem[MA]
• store: mem[MA] ← AC
• push X: SP ← SP - 4; mem[SP] ← X
• pop X: X ← mem[SP]; SP ← SP + 4

Instruction Set

ก่อนอื่น ตกลงกันก่อนว่า ส่วนของ OPCODE เราจะยังไม่ใส่ตัวเลขลงไป แต่สมมติว่ามันกินเนื้อที่ 4 byte (เพื่อให้ง่ายเวลา implement จริงเป็นวงจรด้วย) instruction set ที่เราต้องทำ มีสามกลุ่ม คือ

Fundamental Instructions

PUSH X

• คำสั่งนี้ พิเศษกว่าคำสั่งอื่นตรงที่มันมี operand ด้วย ... ดังนั้น ขนาดของคำสั่งนี้จะต้องรวม X ลงไปด้วย ... เราจะกำหนดให้ 4 byte แรกเป็น opcode และ 4 byte หลังคือ X รวมกันเป็น 8 byte ต่อการ PUSH 1 ครั้ง
• การทำงาน: push X

PBASE

• การทำงาน: push BP

LOAD

• การทำงาน: pop MA; load; push AC

STORE

• การทำงาน: pop AC; pop MA; store

JMP

• การทำงาน: pop PC

JPOS

• การทำงาน: pop AC; if AC > 0, pop PC, else pop AC

JNEG

• การทำงาน: pop AC; if AC < 0, pop PC, else pop AC
  

JZ

• การทำงาน: pop AC; if AC = 0, pop PC, else pop AC

JNZ

• การทำงาน: pop AC; if AC ≠ 0, pop PC, else pop AC

CALL

• การทำงาน: pop AC; push PC + 4; push BP; BP ← SP; PC ← AC
  

RETURN

• การทำงาน: pop AC; SP ← BP; pop BP; pop PC; push AC
  

Dynamic Allocation Instructions

คำสั่งในกลุ่มนี้มีสองคำสั่งคือ ALLOC กับ FREE การทำงานของมันจะพิเศษหน่อย เพราะมันเป็น OS-Level Instruction ดังนั้น จะไม่สามารถ implement เป็น hardware ได้ตรง ๆ

ALLOC

• การทำงาน: pop AC; AC ← malloc(AC); push AC
  

FREE

• การทำงาน: pop AC; free(AC)

Arithmetic and Logical Instructions

พวกนี้ จะมีเยอะเท่าไหร่ก็ได้ ... หลัก ๆ จะมีสองกลุ่มคือ unary กับ binary แต่ถ้าจะทำเพิ่ม ก็ทำได้เรื่อย ๆ นะ

NEG

• การทำงาน: pop AC; push -AC

ADD

• การทำงาน: pop MA; pop AC; push AC + MA

SUB

• การทำงาน: pop MA; pop AC; push AC - MA

MUL

• การทำงาน: pop MA; pop AC; push AC * MA

DIV

• การทำงาน: pop MA; pop AC; push AC / MA

MOD

• การทำงาน: pop MA; pop AC; push AC mod MA

ส่วนคำสั่งที่เป็นด้าน logic เราจะถือว่า 0 = false และ ค่าอื่น ๆ = true นะ (แต่ค่า true ที่เป็น output ของ operation จะกำหนดให้เป็น 1 เลย)

NOT

• การทำงาน: pop AC; push ¬AC

AND

• การทำงาน: pop MA; pop AC; push AC ∧ MA

OR

• การทำงาน: pop MA; pop AC; push AC ∨ MA

IFF

• การทำงาน: pop MA; pop AC; push AC ↔ MA

XOR

• การทำงาน: pop MA; pop AC; push ¬(AC ↔ MA)

NAND

• การทำงาน: pop MA; pop AC; push ¬(AC ∧ MA)

NOR

• การทำงาน: pop MA; pop AC; push ¬(AC ∨ MA)

แล้วจะมาต่อเรื่อง Floating Point อีกทีนะ

มาลองทำ Assembler กัน (Process Space)

ลองสมมติว่า เราเขียนโปรแกรมมา คอมไพล์เสร็จ มันเป็นก้อน object code หน้าตาคงที่ ...

คำสั่ง JMP กับ CALL หละ? ตำแหน่งของการกระโดดมันคงที่หนิ ... แสดงว่า ถ้าเราเอา code เราไปวางไว้ที่อื่น (คือ address เริ่มต้นเปลี่ยนไป) มันก็จะทำงานไม่ถูกน่ะสิ!!!

Frame Pointer

ทางแก้ก็คือ แก้ที่ CPU ของเรา ให้ทุกครั้งที่ทำคำสั่งที่เกี่ยวกับ memory ให้เอาเลขที่ได้ ไปบวกกับ FP ก่อน แค่นี้ก็เรียบร้อย ... ว่าแต่ FP นี่มันจะเก็บไว้ที่ไหนหละ? ... ก็กำหนด Register ขึ้นมาอีกตัวสิ

Process Space

ดังนั้น เพื่อให้การทำงานในแต่ละ process ถูกต้อง เราจะเก็บค่า FP ปะติดกับ object code ไว้สำหรับแต่ละ process ... ค่า FP นั้น จะรู้ในเวลาที่ load โปรแกรมลงใน memory

พอถึงเวลาที่ process นั้นจะทำงาน เราก็เพียงแค่ load ค่า FP ของ process นั้นกลับคืนมา การทำงานก็จะถูกต้องแล้ว

Cross-Process Communication

แล้ว เราจะทำให้ process ต่าง ๆ ติดต่อกันได้ยังไงหละ?

วิธีที่เค้านิยมทำกัน จะมีอยู่ 2 แบบคือ

1. Messaging - ติดต่อผ่าน OS
   
2. Shared Memory - ขอ OS ให้เปิดช่องการติดต่อโดยตรง
   

จริง ๆ ทั้งสองวิธีก็ต้องพึ่ง OS ทั้งคู่ แต่วิธีแรกจะต้องพึ่ง "OS Instruction" มากกว่า

รายละเอียดจริง ๆ ของสองอย่างนี้ จะยังไม่พูดถึงตอนนี้ละกัน ... ไว้หลังจากทำ Virtual Machine กับ Assembler ได้ก่อน

มาลองทำ Assembler กัน (Return Value)

Return Value Problem

สมมติว่า มี code ภาษา C แบบนี้

 int Succ(int a)
 {
  return a + 1;
 }

พอแปลงเป็นภาษา Assembly จะได้

 Succ:
  REF a -2
  PUSH a
  LOAD
  PUSH 1
  ADD
  RETURN

ไม่มีปัญหา แต่ถ้าในฟังก์ชัน มีตัวแปรภายในอยู่หละ?

 int Double(int a)
 {
  int x = a;
  return a + x;
 }

ลองแปลงเป็น Assembly ดู

 Double:
  REF a -2
  VAR 1
  REF x 1
  PVAR x
  PVAR a
  LOAD
  STORE
  PVAR a
  LOAD
  PVAR x
  LOAD
  ADD
  ???
  ???
  RETURN

ที่ใส่ ??? ไว้ก็คือ เราจะ RETURN เลยไม่ได้ เพราะเรายังไม่ได้เรียก FVAR แต่ถ้าเราเรียก FVAR เนี่ย ค่าที่เราต้องการจะ RETURN มันก็จะหายไป เราจะทำยังไงหละ?

เรารู้ว่า ค่าที่จะถูก RETURN ออกไป จะต้องอยู่ในตำแหน่ง BP - 1 แน่ ๆ ดังนั้น เราก็สามารถแก้ปัญหานี้ได้โดย กำหนดตัวแปรที่ตำแหน่ง BP - 1 ให้มันเกินไว้ตัวนึง จะได้เป็น

 Double:
  REF a -2
  PUSH 0
  REF rv 1
  VAR 1
  REF x 2
  PVAR x
  PVAR a
  LOAD
  STORE
  PVAR rv
  PVAR a
  LOAD
  PVAR x
  LOAD
  ADD
  STORE
  FVAR
  RETURN

แต่ ... แบบนี้มันยุ่งยากจัง ... เรากำหนดคำสั่งใหม่มันจะง่ายกว่านะ ... ก็สมมติซะว่าคำสั่ง RETURN มันจะรวม FVAR ไปด้วยเลย แบบนี้

RETURN

1. POP ค่า Return Code ออกมาเก็บไว้ก่อน
2. ถ้า SP ≠ BP ก็ POP ค่าอื่น ๆ ทิ้งไปเรื่อย ๆ จนกว่า SP = BP
3. POP ค่ามาใส่ไว้ใน BP
4. POP อีกค่ามาใส่ไว้ใน PC
5. PUSH ค่า Return Code ที่เก็บไว้ คืนลงไปใน Stack

ข้อดีของการทำแบบนี้ ไม่ใช่แค่เราลดคำสั่ง FVAR ได้แล้ว แต่เรายังประหยัดที่สำหรับ return value ไป 1 ที่ พร้อมกับป้องกันการ POP ไม่หมดได้ด้วย ... code ใหม่ของเราจะเหลือแค่นี้

 Double:
  REF a -2
  VAR 1
  REF x 1
  PVAR x
  PVAR a
  LOAD
  STORE
  PVAR a
  LOAD
  PVAR x
  LOAD
  ADD
  RETURN


มาลองทำ Assembler กัน (Literal)

Literal

ลองดู code ภาษา C ข้างล่างนี้

 int main()
 {
  char *msg = "ABC";
  printf("%s\n", msg);
  return 0;
 }

เราจะแปลงมันเป็นภาษา assembly ได้แบบนี้

 main:
  VAR 1
  REF msg 1
  PVAR msg
  PUSH literal0
  STORE
  PUSH literal1
  PVAR msg
  LOAD
  PUSH printf
  CALL
  FVAR
  PUSH 0
  RETURN
 literal0: "ABC"
 literal1: "%s\n"
 printf:
  ...

สมมติว่า string "ABC" และ "%s\n" ใช้เนื้อที่ตัวละ 1 word เราจะได้ object code สุดท้ายแบบนี้

 0000h: PUSH 0
 0002h: PBASE
 0004h: PUSH 1
 0006h: SUB
 0008h: PUSH 0024h
 000Ah: STORE
 000Ch: PUSH 0025h
 000Eh: PBASE
 0010h: PUSH 1
 0012h: SUB
 0014h: LOAD
 0016h: PUSH 0026h
 0018h: CALL
 001Ah: PUSH 0
 001Ch: MUL
 001Eh: ADD
 0020h: PUSH 0
 0022h: RETURN
 0024h: "ABC"
 0025h: "%s\n"
 0026h: ...

มาลองทำ Assembler กัน (พื้นฐาน)

จริง ๆ แล้ว ภาษา assembly มันก็ภาษาเครื่องแหละ แต่มันเขียนสะดวกกว่านิดนึง ... อะไรที่เราควรจะกำหนดเพิ่มไว้ก่อนหละ? ก็เรื่อง label กับ ตัวแปรไง

Local Variables (อีกแล้ว)

สมมติว่า เราจะเขียนว่า

  void f()
  {
    int x;
    int y;
    x = 0;
    y = x + 500;
  }

เดิมเราจะเขียนว่า

  f:
    VAR 2
    PBASE
    PUSH 1
    SUB
    PUSH 0
    STORE
    PBASE
    PUSH 2
    SUB
    PBASE
    PUSH 1
    SUB
    LOAD
    PUSH 500
    ADD
    STORE
    ...
    FVAR
    PUSH ค่ามั่ว ๆ อะไรก็ได้
    RETURN

จะเห็นว่า การอ้างถึงตัว y จะต้องใช้ 3 คำสั่ง คือ

    PBASE
    PUSH 2
    SUB

เพื่อลดเรื่องยุ่งพวกนี้ เราก็กำหนดภาษาใหม่ แบบนี้

  f:
    VAR 2
    REF x 1 (บอกให้ x = BP - 1)
    REF y 2 (บอกให้ y = BP - 2)
    PVAR x
    PUSH 0
    STORE
    PVAR y
    PVAR x
    LOAD
    PUSH 500
    ADD
    STORE
    ...
    FVAR
    PUSH ค่ามั่ว ๆ อะไรก็ได้
    RETURN

Labels

เราใช้ Label ไปหลายทีแล้วโดยที่ไม่ได้พูดถึง ... จริง ๆ แล้ว การจะกระโดดไปที่ label ต่าง ๆ จำเป็นจะต้องรู้ address ของ label เหล่านั้น ...

ดังนั้น Assembler ของเรา จะต้องมีความสามารถในการ แปลง label เหล่านั้น ให้เป็น address จริง ๆ

สมมติว่ามี code แบบนี้

  int f()
  {
    int x;
    int y;
    do {
      x = ReadFromSomewhere();
      y = ReadFromSomewhere();
    } while (x != y);
    return 0;
  }

จะเขียนเป็น Assembly ได้แบบนี้

  f:
    VAR 2
    REF x 1
    REF y 2
  loop:
    PVAR x
    PUSH ReadFromSomewhere
    CALL
    PVAR y
    PUSH ReadFromSomewhere
    CALL
    PVAR x
    LOAD
    PVAR y
    LOAD
    SUB
    PUSH loop
    JNZ
    FVAR
    PUSH 0
    RETURN

ซึ่ง ตอนที่แปลเป็นภาษาเครื่อง เราจะต้องรู้ 3 อย่างคือ

• ตำแหน่งเริ่มต้นของ f → สมมติว่าเป็น 1234h
• ตำแหน่งเริ่มต้นของ ReadFromSomewhere → สมมติว่าเป็น 5678h
• ขนาดของ instruction → สมมติว่าเป็น 2

จากตำแหน่งเริ่มต้นของ f และขนาดของ instruction เราจะสามารถหาตำแหน่งของ loop ได้ ทำให้สามารถแปล assembly ข้างบนเป็นภาษาเครื่องได้ ดังนี้

  1234h: PUSH
  1236h: PUSH
  1238h: PBASE
  123Ah: PUSH 1
  123Ch: SUB
  123Eh: PUSH 5678h
  1240h: CALL
  1242h: PBASE
  1244h: PUSH 2
  1246h: SUB
  1248h: PUSH 5678h
  124Ah: CALL
  124Ch: PBASE
  124Eh: PUSH 1
  1250h: SUB
  1252h: LOAD
  1254h: PBASE
  1256h: PUSH 2
  1258h: SUB
  125Ah: LOAD
  125Ch: SUB
  125Eh: PUSH 1238h
  1260h: JNZ
  1262h: PUSH 0
  1264h: RETURN

คราวหน้า มาดูเรื่อง Literal กันนะ

มาลองออกแบบ Abstract Instruction Set กัน (ตอนต่อ)

ต่อจาก มาลองออกแบบ Abstract Instruction Set กัน (ตอนแรก) เลยนะ

ครั้งนี้ จะพูดถึงการคำสั่งอย่างย่อ ... เรียกว่า เป็น Higher-Level Assembly ละกัน ... เราจะพัฒนาคำสั่งไปเรื่อย ๆ แบบนี้ จนมันเป็นภาษาชั้นสูงไปเลย

Local Variables

เราสามารถจองตัวแปรบน stack ได้ด้วยคำสั่ง PUSH เช่น สมมติว่าเรามี code ภาษา C แบบนี้

  void f()
  {
    int x;
    int y;
    x = 0;
    y = x + 500;
    ...
  }

เมื่อเราเรียกคำสั่ง f เราจะจองเนื้อที่บน stack ให้กับตัวแปร x และ y ได้ด้วยคำสั่ง PUSH แล้วเมื่อเราจะใช้ตัวแปรพวกนี้ เราก็อ้างถึงจากตำแหน่ง BP (x คือ BP และ y คือ BP - 1) ...

  f:
    PUSH ค่าเริ่มต้นของ x
    PUSH ค่าเริ่มต้นของ y
    PBASE
    PUSH 0
    STORE
    PBASE
    PUSH 1
    ADD
    PBASE
    LOAD
    PUSH 500
    ADD
    STORE
    ...
    POP
    POP
    PUSH ค่าอะไรก็ได้สำหรับ return
    RETURN

แต่เอ๊ะ ... คราวที่แล้วบอกว่า ไม่มีคำสั่ง "POP" หนิ ... แล้วเราจะทำให้มัน POP ได้ไงหละ? ... มันก็ต้องอ้อม ๆ หน่อยแหละ ใช้ความรู้ที่ว่า อะไรคูณ 0 ก็ได้ 0 แล้วก็ อะไรบวก 0 ก็ได้ตัวเดิม เราจะสร้างคำสั่ง POP ได้จาก

  PUSH 0
  MUL
  ADD

แล้วถ้ามี POP หลาย ๆ ตัวติดกัน เราก็แค่เพิ่ม MUL ตรงกลางเข้าไป เช่น

จาก
POP
POP
POP

กลายเป็น

PUSH 0
MUL
MUL
MUL
ADD

Abbreviated Form

เพื่อให้เขียนง่าย แทนที่เราจะเขียน PUSH ซ้ำ ๆ สำหรับตัวแปรหลาย ๆ ตัว เราจะเขียนว่า

VAR n

เพื่อหมายถึงการ PUSH เปล่า ๆ ไป n ครั้ง เป็นเนื้อที่ของตัวแปร n ตัว ส่วนการ POP เราก็จะเขียนว่า

FVAR

(ย่อมาจาก Free VAR) เพื่อหมายถึง PUSH 0, MUL, MUL, MUL, ..., ADD ที่มีจำนวน MUL เท่ากับ n ของคำสั่ง ALLOC ก่อนหน้านี้

Dynamic Allocation

เนื่องจาก ... การจองเนื้อที่สำหรับตัวแปรบน heap เป็นสิ่งที่ทำกันบ่อยมาก ๆ เราก็เลย สมมติว่ามีคำสั่งสำหรับทำงานนี้เลยละกัน

ALLOC

การทำงานคือ

• POP ค่าบนสุดของ Stack ออกมา ให้เป็นขนาด memory block ที่ต้องการ
• ไปค้นหาเนื้อที่ว่างจาก heap
• PUSH ค่า address คืนลงไปใน Stack

เพื่อให้การคืน memory ทำได้ง่ายขึ้น เราจะจองเนื้อที่ให้เกินที่ขอไปนิดนึง เพื่อใส่ขนาดของ block ไว้ข้างหน้า address ที่คืนออกมา ผลก็คือ คำสั่ง

FREE

จะต้องการ POP ค่าจาก stack เพียงค่าเดียว คือ address

ตัวอย่างเช่น

  void f()
  {
    int* x;
    x = new int;
    ...
  }

  f:
    VAR 1 (สมมติว่าขนาดของ pointer = 1)
    PBASE
    PUSH 1 (สมมติว่าขนาดของ int = 1)
    ALLOC
    STORE
    ...
    FVAR
    PUSH ค่าอะไรก็ได้สำหรับ return
    RETURN

สรุปคำสั่งตอนนี้

จริง ๆ คำสั่ง ALLOC กับ FREE มันไม่ใช่คำสั่งพื้นฐานที่ CPU ควรจะมีหรอกนะ มันเป็น OS-level Instruction หนะ วิธีสร้าง ALLOC กับ FREE จริง ๆ ไว้จะบอกทีหลัง แต่ตอนนี้สมมติว่ามีให้ใช้เลยละกัน

Minimal Instruction Set + ALLOC & FREE

PUSH
PBASE
LOAD
STORE
JPOS
CALL
RETURN
NAND
NEG
ADD
MUL
ALLOC
FREE

Abbreviations
JMP
JNEG
JZ
JNZ
NOT
AND
OR
XOR
IFF
SUB
DIV
MOD
VAR
FVAR
...

แล้วจะมาเพิ่ม abbreviation อีกเรื่อย ๆ นะ

มาลองออกแบบ Abstract Instruction Set กัน (ตอนแรก)

ขอโทษล่วงหน้า ถ้าทำให้ใครบางคนอ่านเรื่องนี้ไม่รู้เรื่องตั้งแต่ต้น ...

บังเอิญว่า อยากจะเอาเรื่องเกี่ยวกับการออกแบบ Instruction Set ของ CPU มาให้ดู ๆ กันบ้างหนะ

Abstract Instruction Set

จุดประสงค์การออกแบบชุดคำสั่ง (Instruction Set) นี้ ไม่ใช่เพื่อให้มันประสิทธิภาพสูงสุด หรือว่าทำเป็นวงจรง่ายหรอกนะ แต่ อยากจะทำให้มันทำงานได้ครบ โดยที่มีคำสั่งน้อย ๆ มากกว่า

Chosen Design: Stack Machine

Stack Machine เป็นแนวคิดที่ว่า Operation ทั้งหลาย ทำบน Stack ... คิดว่าแบบนี้น่าจะทำให้ลดจำนวนคำสั่งลงได้เยอะ

ข้อเสียก็คือ การจะทำอะไรอย่างนึง มันต้องมีหลายคำสั่งน่ะสิ แล้วก็ การทำ Pipelining จะยากด้วย แต่ขอไม่สนเรื่องนี้ก่อน

เหตุผลสนับสนุนอีกอย่างนึงที่ทำให้เลือก Operation on Stack ก็คือ เวลาทำ compiler ให้แปล source code เป็น machine code เนี่ย มันจะค่อนข้างง่ายและตรงมาก (แต่ประสิทธิภาพก็ไม่ได้ดีเท่าไหร่แหละ)

First Two Opcodes: PUSH and POP

เวลาจะทำ Stack ใคร ๆ ก็ต้องคิดถึง Push กับ Pop แน่ ๆ เราก็กำหนดเลยละกันว่า เราจะมีสองคำสั่งนี้

ผลก็คือ เราสามารถสร้างให้คำสั่งอื่น ๆ ไม่รับ operand เองโดยตรงได้ เช่น

คำสั่ง A = B + C

Instruction Set ทั่วไป
ADD A, B, C

Stack-based Operation ของเรา
PUSH B
PUSH C
ADD
POP A

ว่าแต่ว่า ... เราจะระบุสิ่งที่จะ PUSH กับ POP ได้ยังไงหละ?

Types of Operands

เนื่องจากเราจะลดความซับซ้อนให้เหลือน้อยที่สุด เราจะยอมให้มี operand ได้แค่แบบเดียวแบบ คือ

• Immediate

ไว้จะมาอธิบาย ว่า addressing แบบอื่น สามารถทำได้จากสองแบบนี้ แต่เราต้องพึ่งคำสั่งอื่น ๆ เช่น LOAD กับ ADD

Required Registers

เราจะให้มี register เพียง 3 ตัว ที่สามารถยุ่งเกี่ยวได้ด้วย machine instruction คือ

• Program Counter (PC) = Address ของคำสั่งปัจจุบัน
  
• Base Pointer (BP) = Address แรกของ Local Variable ปัจจุบัน
  
• Stack Pointer (SP) = Address ของ Top-of-stack
  

โดยทั้งสามตัวนี้ ควรจะใช้ Address Space เดียวกัน (Virtual ก็ได้)

สมมติว่า SP จะลดค่าเมื่อ PUSH และเพิ่มค่าเมื่อ POP นะ (ทำตามแบบที่เค้านิยมกัน)

Indirect Indexing: PBASE

เนื่องจาก Base Pointer (BP) เป็น register ที่ควรจะสามารถนำค่าไปบวก-ลบได้ ดังนั้น เราจึงควรจะสร้างคำสั่งที่ใช้อ่านค่า BP ดังนี้

PBASE = Push ค่าของ BP ขึ้น Stack

LOAD and STORE

เราจะกำหนดให้ คำสั่ง LOAD จะใช้ operand เป็นตัวบนสุดของ stack ตัวเดียว มีการทำงานคือ

1. เอาค่าบนสุดของ stack ไปเป็น address อ้างอิง memory
2. อ่านค่าจาก memory ในตำแหน่งนั้น
3. เอาค่าที่อ่านได้ มาแทนที่ในตำแหน่งบนสุดของ stack (ที่เคยเป็น address)

ส่วนคำสั่ง STORE จะใช้ operand 2 ตัว มีการทำงานคือ

1. POP ตัวแรกออกจาก stack ใช้เป็น address อ้างอิง memory
2. POP ตัวที่สองออกจาก stack ใช้เป็นค่าที่จะเขียนลง memory
3. เขียนค่าที่ได้ (จากการ POP ครั้งที่สอง) ลงใน memory (address ได้จากการ POP ครั้งแรก)

จะว่าไป ... LOAD มันก็คือ PUSH แล้ว STORE มันก็คือ POP น่ะแหละ

สังเกตดี ๆ หละ ว่า จริง ๆ เราไม่ต้องมีคำสั่ง POP นะ!!!

Logical Functions: NOT, AND, OR, XOR, IFF

ถึงแม้ว่า จริง ๆ แล้วเราสามารถใช้แค่ NAND หรือ NOR เพียงอย่างเดียวได้ แต่ตรงนี้ ไม่ขอประหยัดจำนวน Opcode นะ เพราะว่ามันไม่ได้เป็นสาระสำคัญเท่าไหร่ (ถ้าอยากจะสร้างแบบประหยัด ให้มันมีแต่ NAND หรือมีแต่ NOR เวลาทำ compiler ก็จะเหนื่อยหน่อย เท่านั้นเอง)

Arithmetic Functions: NEG, ADD, SUB, MUL, DIV, MOD, EXP, LOG, ...

พวกนี้ก็เหมือนกัน ... จริง ๆ มีแค่ NEG ADD แล้วก็ MUL ก็น่าจะพอแล้ว แต่การประหยัดจำนวนคำสั่งตรงนี้ ก็ไม่ใช่สาระสำคัญเหมือนกัน ดังนั้นเราจะถือว่า คำสั่งพวกนี้ มีหมดเลย ก็แล้วกัน

Classical Modes of Addressing

เนื่องจาก Operand เรา มีแต่แบบ Immediate การอ้างถึง Operand ในลักษณะอื่น ๆ แบบที่เครื่องทั่ว ๆ ไปเค้าทำได้ มันจะต้องใช้หลายคำสั่งหน่อยนะ เช่น

Target: Value at memory address X
Abbreviation: [X]
How to PUSH that?
PUSH X
LOAD

Target: Value at memory address BP + X
Abbreviation: [BP + X]
How to PUSH that?
PBASE
PUSH X
ADD
LOAD

Target: Value at memory address (BP + value at X)
Abbreviation: [BP + [X]]
How to PUSH that?
PBASE
PUSH X
LOAD
ADD
LOAD

Target (in C): Array[Index]
Abbreviation: [BP + array + [BP + index]]
How to PUSH that?
PBASE
PUSH array
ADD
PBASE
PUSH index
ADD
LOAD
ADD
LOAD

Simple Branch Instructions: JMP, JPOS, JNEG, JZ, JNZ

• JMP: POP → PC
• JPOS: POP → เก็บไว้ แล้ว POP อีกที ถ้าได้ค่าเป็นเลขบวก (มากกว่า 0) ถึงจะกระโดดไปยัง address ที่เก็บไว้
• JNEG: คล้าย ๆ กับ JPOS แต่จะกระโดดถ้าค่าที่ POP ออกมาครั้งที่ 2 เป็นเลขติดลบ
  
• JZ: POP → เก็บไว้ แล้วก็ POP อีกที ถ้าได้ค่าเป็น 0 ถึงจะโดดไปยัง address ที่เก็บไว้
• JNZ: คล้าย ๆ กับ JZ แต่เงื่อนไขการกระโดดตรงกันข้าม

จริง ๆ จะมีแต่ JPOS ก็ได้แหละ ที่ไม่ตัดตัวอื่นออก ก็เพราะว่ามันไม่ใช่สาระสำคัญ (อีกแล้ว)

Subroutine: CALL, RETURN

คำสั่ง CALL จะวุ่น ๆ หน่อย เพราะมีการทำงานหลายขั้น คือ

1. POP ค่า address ที่จะกระโดดไป เก็บไว้
2. PUSH ค่า PC + 1 ไว้
3. PUSH ค่า BP ไว้
4. กำหนดค่าให้ BP = SP
5. กำหนดค่าให้ PC = address ที่ POP ไว้ตอนแรก (ซึ่งก็คือ การกระโดดนั่นเอง)

ส่วนคำสั่ง RETURN จะทำงานกลับกันกับ CALL คือ

1. POP ค่า Return Code ออกมาเก็บไว้ก่อน
2. POP ค่ามาใส่ไว้ใน BP
3. POP อีกค่ามาใส่ไว้ใน PC (ซึ่งก็คือ การกระโดดกลับ)
4. PUSH ค่า Return Code คืนลงไปใน Stack

จริง ๆ แล้ว ตอนที่ RETURN จะไม่เผื่อที่สำหรับ Return Code ก็ได้ แต่อันนี้เผื่อไว้เพื่อความสะดวกหนะ

Local Variable and Parameters

ถ้าต้องการส่งผ่าน parameter ให้กับ function เราก็จะใช้วิธี PUSH ใส่ stack ไว้ก่อน เช่น

1. PUSH A
2. PUSH B
3. PUSH CustomAdd
4. CALL

• ถ้า BP หลัง CALL = x
• SP ก่อน CALL จะ = x + 1
• ตำแหน่งของ B ก็เลย = x + 2
• และ ตำแหน่งของ A ก็ = x + 3

สรุปก็คือ parameter ตัวที่ PUSH มาหลังสุด (ไม่นับ address ของฟังก์ชัน ซึ่งในตัวอย่างนี้คือ CustomAdd) จะมี address เป็น BP + 2

CustomAdd:

1. PBASE
2. PUSH 2
3. SUB
4. LOAD
5. PBASE
6. PUSH 3
7. SUB
8. LOAD
9. ADD
10. RETURN

สรุปคำสั่ง

ชุดคำสั่งเล็กสุด
PUSH
PBASE
LOAD
STORE
JPOS
CALL
RETURN
NAND
NEG
ADD
MUL

คำสั่งลดความเหนื่อย
JMP
JNEG
JZ
JNZ
NOT
AND
OR
XOR
IFF
SUB
DIV
MOD
...

ตอนนี้เราก็ได้ Instruction Set คร่าว ๆ แล้ว แต่เราไม่พูดถึงขนาดของข้อมูลในแต่ละช่องของ Stack เลยนะเนี่ย ... ก็เลยเรียกว่า Abstract Instruction Set ไงหละ

การบวกลบเลขจำนวนเต็มไม่ติดลบ

เนื่องจาก การคิดเลขในฐานอะไรก็เหมือนกันหมด แต่เราอยากทำในกรณีที่มันเป็นฐาน 2 เพราะว่า คอมพิวเตอร์มันเป็นฐานสอง ... มาดูกันว่า การบวกเลขฐานสอง ทำกันยังไงนะ

จริง ๆ แล้ว ก็เหมือนกับฐาน 10 น่ะแหละ แต่มันง่ายกว่าด้วยซ้ำ เพราะว่า ผลลัพธ์มีแค่ 0 กับ 1 ดังนั้น ความเป็นไปได้ทั้งหมดของการบวกกันในแต่ละหลัก คือ ... (ตัวทด ใช้สีแดงนะ)

กรณีที่ไม่มีตัวทด (ตัวทด = 0)
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10

กรณีที่มีตัวทด (ตัวทด = 1)
1 + 0 + 0 = 01
1 + 0 + 1 = 10
1 + 1 + 0 = 10
1 + 1 + 1 = 11

พอได้การบวกทุกแบบแล้ว เราก็ลองเอามาใช้ดู

ตอนนี้ก็บวกเป็นละ ... แล้วการลบหละ?

เลขจำนวนเต็มไม่ติดลบ

ที่ผ่าน ๆ มา เราก็รู้กันไปเรียบร้อยแล้วเรื่อง การแปลงฐานเลข คราวนี้ก็ ขอตั้งข้อกำหนดเบื้องต้นไว้นิดนึงนะ คือ

ข้อมูลในคอมพิวเตอร์ จะอยู่ในรูปลำดับของเลขฐานสอง ที่มีความยาวจำกัด
ความยาวของลำดับ = จำนวน bit ของข้อมูล

แล้วก็ ขอกำหนดคำที่จะใช้เพื่อให้คุยกันง่ายขึ้น คือ

ข้อมูล n bit = เลขฐานสอง n หลัก

จำนวนเต็มไม่ติดลบ ที่สามารถแทนได้ด้วย n bit

คิดด้วยหลักการง่าย ๆ ว่า ข้อมูล 1 bit สามารถเป็นได้ 2 แบบ คือ 0 กับ 1 ดังนั้น

ข้อมูล n bit สามารถเป็นได้ 2ⁿ แบบที่แตกต่างกัน

เนื่องจาก จำนวนเต็มที่ไม่ติดลบ 2ⁿ ตัวแรก ก็คือ

0, 1, 2, ..., 2ⁿ - 1

ดังนั้น ข้อมูล n bit จะสามารถแทนจำนวนเต็มไม่ติดลบที่มีค่าน้อยกว่า 2ⁿ ได้ 1 ตัว

Byte

1 byte = 8 bits

ดังนั้น ข้อมูล 1 byte จะแทนจำนวนเต็มไม่ติดลบที่มีค่าน้อยกว่า 2⁸ ได้ 1 ตัว

หมายเหตุ: แทนที่จะมองว่า 1 byte = เลขฐานสอง 8 หลัก เราอาจจะมองว่า 1 byte = เลขโดดฐาน 256 ก็ได้

เลขฐาน 16

ในโปรแกรมคอมพิวเตอร์พวกที่ให้เห็นค่าใน memory เรามักจะเห็นเลขฐาน 16 กันบ่อยพอควร แล้วมันก็จะอยู่เป็นคู่ ๆ ด้วย สาเหตุที่เค้านิยมเขียนเลขฐาน 16 อยู่เป็นคู่ ๆ ก็เพราะว่า มันสั้นกว่าการเขียนเป็นเลขฐานสอง แล้วที่มันใช้ได้ก็เพราะว่า

2⁴ = 16 → เลขฐาน 16 ยาว 1 หลัก = ข้อมูล 4 bit
16 × 16 = 256 → เลขฐาน 16 ยาว 2 หลัก = ข้อมูล 1 byte

ดังนั้น

เลขฐาน 16 ยาว 2 หลัก = 1 byte

ตัวอย่าง

1010₂ = A₁₆ = 10
1101₂ = D₁₆ = 13
1010 1101₂ = AD₁₆ = 173

ความนิยมอีกเรื่อง

เนื่องจาก การจะเขียนฐานเลขห้อย ๆ เนี่ย บางทีมันทำยาก (เช่น ในคอมพิวเตอร์สมัยก่อน หรือในหน้าจอของเครื่องอะไรก็ตามที่เป็น Text Mode) เค้าเลยนิยมเอา h ห้อยท้ายแทน (h มาจาก hexadecimal ← hexa + dec = 6 + 10) ส่วนเลขฐานสอง บางที่ก็เอา b ห้อยท้ายแทนการห้อยสอง เช่น

ADh = 173
11011010b = DAh = 218

จริง ๆ เครื่องหมายอื่น ๆ ก็มีอีก ไว้จะค่อย ๆ เอามาให้ดูบ้างละกันนะ

เลขฐานสอง - ทำไมต้อง 2

ทำไมคอมพิวเตอร์ถึงนิยมใช้เลขฐาน 2 ???

เอามาให้ดูเล่น ๆ ขำ ๆ นะ อย่าซีเรียสมาก แต่บางอันมันก็มีเค้านะ

ทางฟิสิกส์

• ประจุมีสองขั้ว คือ บวกกับลบ เกิดจากอนุภาคสองชนิดคือ Electron และ Proton
  
• แหล่งกำเนิดไฟฟ้ามีสองขั้ว วงจร Digital ก็เลยทำได้ง่ายที่สุดเมื่อสนใจศักย์ไฟฟ้าเพียง 2 ระดับ

ทางคณิตศาสตร์

• เลขฐาน 1 ใช้ไม่ได้ (เพราะ d(i) = 1 สำหรับทุก i) เลขฐาน 2 ก็เลยเป็นฐานต่ำสุดที่ใช้ได้
• complement ทำง่ายดี
  
• วิธีหารเลขฐาน 2 ไม่มีการคูณในขั้นตอน
• 2 เป็นจำนวนเฉพาะตัวแรก (อันนี้ไม่ค่อยเกี่ยวแล้ว :P)
  
• สมการพหุนามกำลังต่ำที่สุดที่สามารถมีคำตอบเป็นจำนวนเชิงซ้อน คือ 2
• สูตรเส้นรอบวงของวงกลมคือ สองπr และสูตรพื้นที่ก็คือ πr^สอง (เริ่มนอกเรื่องมากขึ้น)
  

ด้านอื่น ๆ (หลุดเรื่องไปแล้ว)

• สิ่งมีชีวิตทุกสายพันธุ์ยกเว้นคน มีเพศไม่เกิน 2 เพศ (หรืออย่างน้อย เราก็รู้แค่นี้ ... สัตว์มันอาจจะรู้กันเองก็ได้เนอะ)
• อวัยวะของเรา มันจะมีเป็นคู่ ๆ
• ประสาทการมองเห็นของเรา เป็นภาพสองมิติ สองภาพ
  
• ภาค สอง ของ The Lord of the Rings ชื่อว่า The Two Towers
• "น้องพลับขอสอง" (... พี่พลับขอเท่าไหร่อะวาว?)
  
• ปาท่องโก๋ แซนด์วิช แฮมเบอร์เกอร์
• ยังไม่มีเพลงชื่อว่า สามรัก สี่รัก ... n รัก นอกจาก 2
• โจ้หญิงทำโทรศัพท์หายไปแล้วสองเครื่อง
  
• http://tunococ.blogspot.com/ กับ http://www.geocities.com/tunaococ/ อยู่กันเป็นคู่

คราวนี้เพ้อเจ้อมากไปละ :D ไว้จะมาเจาะเรื่อง 1's complement กับ 2's complement กันอีกทีนะ

การแปลงฐานเลข - ส่วนทศนิยม

ต่อเลยละกันนะ ... คราวนี้สมมติว่าค่า X ของเรา เป็นจำนวนจริงบวก มีส่วนจำนวนเต็มและส่วนทศนิยมอยู่ เราจะแยกสองส่วนนี้ออกจากกัน โดยสมมติให้

X = W + F

เมื่อ W ∈ Z⁺ ∪ {0} และ F ∈ [0, 1)

คราวนี้ สมมติให้ s เป็นการเขียนค่า X ในระบบเลขฐาน n เราจะรู้ว่า

X = Σ_i∈Z s(i) nⁱ

ถ้ากำหนดให้

W = Σ_i∈Z s_w(i) nⁱ
F = Σ_i∈Z s_f(i) nⁱ

สมการแรก จะเขียนได้เป็น

W + F = Σ_i∈Z [s_w(i) + s_f(i)] nⁱ

จากตอนที่แล้ว (การแปลงฐานเลข - จำนวนเต็ม) ที่เรารู้ว่า s_w(i) = 0 เมื่อ i < 0

และเนื่องจาก 0 ≤ F < 1 ทำให้รู้ว่า s_f(i) = 0 เมื่อ i ≥ 0

ดังนั้น เราจะแยกคิด s_w(i) กับ s_f(i) ได้ ...

วิธีการหา s_w(i) ก็รู้แล้ว เราจะสนใจแต่ s_f(i) นะ ... เริ่มจากสมการนี้

F = Σ_i<0 s_f(i) nⁱ
F = Σ_i>0 s_f(-i) n^-i

คูณตลอดด้วย n จะได้

nF = Σ_i>0 s_f(-i) n^-i+1

เพราะว่าเรารู้ว่า s_f(-i) ทุกตัว มีค่าไม่เกิน n - 1 ดังนั้น

Σ_i>1 s_f(-i) n^-i+1 ≤ Σ_i≥2 (n - 1) n^-i+1
Σ_i≥1 (n - 1) n^-i = 1

เราจึงแยกส่วนจำนวนเต็มกับส่วนทศนิยมได้ ดังนี้

nF = s_f(-1) + Σ_i>1 s_f(-i) n^-i+1

ผลรวมใน Σ ทางขวา จะอยู่ในช่วง [0, 1) ดังนั้น s_f(-1) = nF mod 1

ได้มาตัวนึงละ ... ทำต่อนะ ... เอา s_f(-1) ลบออกจากทั้งสองข้าง

nF - s_f(-1) = Σ_i>1 s_f(-i) n^-i+1

ค่าทั้งสองข้างของสมการ จะมีค่าอยู่ในช่วง [0, 1) เราก็เอา n คูณเข้าไปอีกที แล้วแยกส่วนเต็มกับเศษออกจากกันอีกที

n[nF - s_f(-1)] = Σ_i>1 s_f(-i) n^-i+2
n[nF - s_f(-1)] = Σ_i>0 s_f(-i - 1) n^-i+1
n[nF - s_f(-1)] = s_f(-2) + Σ_i>1 s_f(-i - 1) n^-i+1

พจน์ที่ติด Σ อยู่ด้านขวา ก็จะรวมกันได้ไม่ถึง 1 อีก ... ดังนั้น s_f(-2) = n[nF - s_f(-1)] mod 1

ถ้าเราทำซ้ำ ๆ ไปเรื่อย ๆ เราก็จะหาค่า s_f(-i) ได้ทั้งหมด

การแปลงฐานเลข - จำนวนเต็ม

คราวที่แล้ว พูดถึง d_n กับ s ไปแล้ว เราก็รู้แล้วหละ ว่าค่าของเลขในระบบฐานต่าง ๆ กัน มันคิดยังไง คราวนี้เราจะมาดูการแปลงกลับมั่งนะ

ในตอนนี้ จะพูดถึงกรณีที่ไม่มีทศนิยม (จำนวนเต็ม) อย่างเดียวก่อน ...

สมมติว่าเรามีค่า X อยู่

เราอยากรู้ว่า ในระบบเลขฐาน n เราจะหาค่า s(i) ต่าง ๆ ได้ยังไง ... ความสัมพันธ์ของ X กับ s ก็คือ

X = Σ_i≥0 s(i) nⁱ

เริ่มต้นโดย หาค่า s(0) ก่อน โดยพิจารณาที่ mod n

X ≡ Σ_i≥0 s(i) nⁱ (mod n)
X ≡ s(0) (mod n)

ถ้าเราให้ s(i) ทุกตัวอยู่ในช่วง 0 ถึง n - 1 เราจะรู้ทันทีว่า s(0) = X mod n

พอรู้แล้ว เราก็เอา s(0) ลบออกจากสองข้างของสมการตั้งต้น ได้เป็นแบบนี้

X - s(0) = Σ_i≥1 s(i) nⁱ = n Σ_i≥0 s(i + 1) nⁱ

แสดงว่า ทั้งสองข้างของสมการ หารด้วย n ลงตัว ... เราก็หารซะ

(X - s(0)) / n = Σ_i≥0 s(i + 1) nⁱ

พิจารณาที่ mod n อีกครั้ง เราจะเห็นว่า

(X - s(0)) / n ≡ Σ_i≥0 s(i + 1) nⁱ (mod n)
(X - s(0)) / n ≡ s(1) (mod n)

เราก็จะสรุปได้ว่า s(1) = [(X - s(0)) / n] mod n

สังเกตว่า ถ้าเราทำซ้ำไปเรื่อย ๆ เราก็จะหา s(i) ได้ทั้งหมด

จะว่าไป ... มันก็มีส่วนคล้าย ๆ Taylor Series กับ Newton Polynomial นะเนี่ย (ลองดู Discrete vs Continuous: Taylor Series และ Newton Polynomial สิ)

เลขฐาน - มันเป็นไงในคณิตศาสตร์

คราวนี้ ขอเปิดตัวเรื่องใหม่ ที่สามารถเขียนตอนละสั้น ๆ ได้ :P

ก็ ... ไหน ๆ ผมก็จะเรียน Computer Science อยู่แล้ว เริ่มสังเกตว่า ... ทำไมไม่ค่อยเขียนเรื่องคอมพิวเตอร์มั่งเลย!!!

ตอนนี้เลยขอเริ่มล่ะนะ ... เกริ่นเรื่องเลขฐานก่อน

ระบบเลขฐาน n

เลขโดดในระบบเลขฐาน n คือ 0, 1, 2, ..., n - 1 เช่น

ในระบบเลขฐาน 2 เราจะมีเลขโดด 2 ตัว คือ 0 กับ 1

ในระบบเลขฐาน 16 เราจะมีเลขโดด 16 ตัว คือ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 และ 15

ความนิยม ... ตัว A B C D E F

ก็ไม่มีอะไรหรอก เพียงแต่ว่า เวลาเค้าเขียนเลขฐาน 16 กัน มันจะสะดวกกว่า ถ้าให้

A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

เพราะเวลาเขียนจริง ๆ มันใช้เนื้อที่หลักเดียว ... เราไม่ต้องมาคอยเว้นวรรค เพื่อให้มันชัดเจน เช่น

"10 15 2"

ก็จะกลายเป็น

"AF2"

ทำให้เขียนได้สั้นลง

ค่าประจำหลัก

เพื่อให้ง่ายต่อการเขียน เราจะเขียนค่าประจำหลักที่ i ว่า d_n(i) โดยที่

d_n(i) = nⁱ

ดังนั้น ค่าประจำหลักที่ 0 ก็คือ 1 ไม่ว่า n จะเป็นเท่าไหร่

ตัวเลข

เราจะมองตัวเลขที่เราเขียน ๆ กัน เป็นฟังก์ชันของเลขหลัก ชื่อว่า s(i) แบบนี้

ถ้าเขียน s = "123" จะแปลว่า
s(0) = 3
s(1) = 2
s(2) = 1
s(อื่น ๆ) = 0

ถ้าเขียน s = "2.345" จะแปลว่า

s(0) = 2
s(-1) = 3
s(-2) = 4
s(-3) = 5
s(อื่น ๆ) = 0

ค่าจริง ๆ ของตัวเลข

ค่าจริง ๆ ของตัวเลข s บนฐาน n ก็คือ

Σ_i∈Z s(i) d_n(i)

ซึ่ง ... ถ้ามอง s กับ d_n เป็นเวกเตอร์ มันก็คือ

s ⋅ d_n

นั่นเอง

โจทย์คลายเครียด

ขออภัยเป็นอย่างยิ่ง ที่ไม่สามารถ update ได้เป็นเวลานานมาาาาาาาก ... T_T

เพื่อให้สามารถชดเชยส่วนที่หายไปได้ ... ขอเขียนเรื่องละสั้น ๆ แล้วก็ เนื้อหาน้อย ๆ หน่อยนะ

คราวนี้ ได้โจทย์มาทาง E-mail ... โจทย์มีอยู่ว่า

กำหนดให้
A₁ = 1
A₂ = 2
และ A_n = A_n-1 + A_n-2
จงพิสูจน์ว่า A_n < (7/4)ⁿ เมื่อ n ≥ 1

พิสูจน์ด้วยการอุปนัยทางคณิตศาสตร์

ลองแทนค่ากรณีเริ่มต้น คือ n = 1 และ n = 2 จะเห็นว่า

A₁ = 1 < 7/4
A₂ = 2 < 49/16

คราวนี้ สมมติว่า A_n < (7/4)ⁿ สำหรับทุก n ที่ 1 ≤ n < k เราจะรู้ว่า

A_k = A_k-1 + A_k-2
A_k < (7/4)^k-1 + (7/4)^k-2
A_k < (7/4)^k-2(7/4 + 1)
A_k < (7/4)^k-2(11/4)

เนื่องจาก 11/4 = 44/16 < 49/16 = (7/4)² ดังนั้น

A_k < (7/4)^k-2(7/4)² = (7/4)^k

แสดงว่า A_n < (7/4)ⁿ เป็นจริงเมื่อ n = k ด้วย

เราก็เลยสรุปได้ว่า มันเป็นจริงสำหรับทุก n ≥ 1

Suffixes: -ascence, -iscence

คราวที่แล้ว พูดถึง -escence ไปแล้ว คราวนี้ เก็บตกอีกนิดนึงละกัน

-ascence

จะว่าไป suffix ตัวนี้ มีแค่คำเดียวเอง คือ nascence (อีกตัวนึง เกิดจากเอา re- ไปเติม) แต่ความหมายก็คล้าย ๆ กันกับ -escence นะ ... ดูเลยดีกว่า

• nascence [n] = event of being born
• nascent [adj] = coming into existence

• re'nascence [n] = revival of learning and culture
• re'nascent [adj] = surging or sweeping back again

แล้วก็ มาดู suffix อีกตัว

-iscence

สำหรับ suffix ตัวนี้ มีคำอยู่ทั้งหมด 4 คำนะ คือ...

con'cupiscence ← 'concubine [n] = ภรรยาไม่จดทะเบียน | เมียน้อย

• con'cupiscent [adj] = having sexual lust = libidinous, lustful, lecherous, salacious
• con'cupiscence [n] = sexual desire
• con'cupiscible [adj] = exciting desire

de'hiscence

• de'hisce [v] = burst or split open
• de'hiscent [adj] = (ผล/ฝัก/ฯลฯ) เปิดออกเพื่อปล่อยเมล็ด (หรือสปอร์) เมื่อถึงเวลา
• de'hiscence [n] = การเปิดออก เพื่อปล่อยเมล็ด (หรือสปอร์)

inde'hiscence

• inde'hiscent [adj] = ไม่ dehiscent
• inde'hiscence [n] = ความ indehiscent

remi'niscence ← re'mind

• remi'nisce [v] = นึกถึงอดีต
• remi'niscent (of) [adj] = ทำให้นึกถึง
• remi'niscence [n] = การระลึกถึงอดีต
• remi'niscential [adj] = เกี่ยวกับความทรงจำ

Suffix: -escence

คำที่ลงท้ายด้วย -escence ทั้งหมด เป็นคำนาม มีความหมายประมาณว่า "การค่อย ๆ เป็น" หรือ "กำลังจะเป็น" โดยคำส่วนใหญ่ จะมีรูป adjective เป็น -escent

ที่เอามาให้ดูนี่ จริง ๆ ไม่หมดนะ แต่ก็ส่วนใหญ่หละ ... ส่วนคำเกี่ยวข้องที่ใส่ให้เนี่ย จริง ๆ อาจจะไม่ได้เป็นที่มาที่ถูกต้อง แต่มันก็พอจะช่วยจำได้หละนะ

acqui'escence ← acquit

• ac'quit [v] = exculpate, exonerate
• acqui'esce [v] = เห็นด้วย โดยไม่โต้แย้ง (และอาจจะสนับสนุน)
• acqui'escent [adj] = willing to acquiesce
• acqui'escence [n] = การ acquiesce
  

ado'lescence ← adult

• ado'lescent [adj] = กำลังจะเป็นผู้ใหญ่
• ado'lescent [n] = วัยรุ่น
• adolesce [v] = เข้าสู่ช่วงวัยรุ่น
• ado'lescence [n] = ช่วงวัยรุ่น

arbo'rescence ← arbor/arbour [n] = ต้นไม้ (ที่ไม่เป็นพุ่ม)

• arbo'rescent [adj] = มีกิ่งก้านสาขา เหมือนต้นไม้ = ar'boreal, ar'boreous, arboresque, arboriform
• arbo'rescence [n] = สภาวะ arborescent (มักใช้กับการตกผลึก)

coalescence ← coalition

• coalition [n] = กลุ่มคน, องค์กร | การรวม (สิ่งที่ต่างกัน) เข้าด้วยกัน
• coalesce [v] = เติบโตด้วยกัน | อยู่ร่วมกัน
• coalescent [adj] = coalescing
• coalescence [n] = การรวม (สิ่งที่ต่างกัน) เข้าด้วยกัน

con'crescence ← concrete

• concrete [v] = ฉาบซีเมนต์ | ทำให้แข็งขึ้น, ทำให้แน่นขึ้น, coalesce
• con'crescence [n] = การก่อตัวจากอนุภาคเล็ก ๆ หลาย ๆ อนุภาค มาเกาะเข้าด้วยกัน
  

conva'lescence

• conva'lesce [v] = ฟื้นฟูจากความเจ็บป่วย
• conva'lescent [n] = ผู้ป่วยที่กำลังรักษาตัวอยู่
• conva'lescent [adj] = การ convalesce | เกี่ยวกับ convalescent [n]
• conva'lescence [n] = recovery, recuperation

deca'lescence ← -cal- = ความร้อน

• deca'lescence [n] = ชื่อปรากฏการณ์ เมื่อโลหะได้รับความร้อนแล้วอุณหภูมิไม่เพิ่ม เพราะพลังงานที่ได้รับ สูญเสียไปในการเปลี่ยนแปลงโครงสร้างผลึก

defer'vescence ← de-, fever

• defer'vesce [v] = ไข้ลด
• defer'vescence [n] = การลดลงของไข้

deli'quescence ← de-, liquid

• deli'quesce [v] = สลายตัว | ละลายหายไป
• deli'quescent [adj] = (มักใช้กับเกลือ) ละลายเมื่อได้รับความชื้นในอากาศ
• deli'quescence [n] = การ deliquesce

detu'mescence ← de-, tumor

• tumor [n] = เนื้องอก
• tumid [adj] = บวม | โตเกินความจำเป็น, ผิดปกติ → tumidity [n]
• detu'mescence [n] = การหดตัวของส่วน/สิ่งที่บวม

effer'vescence ← effuse [v] = เท | ไหล | emit, give out

• effervesce [v] = ทำให้เกิดฟอง, ตีให้เป็นฟอง
• effer'vescent [adj] = มีฟอง, เป็นฟองได้ง่าย | (เครื่องดื่มหรือน้ำ) มี CO₂ อยู่เยอะ, (น้ำหวาน) อัดลม | กระตือรือร้น, สดชื่น
• effer'vescence [n] = การ effervesce | คุณสมบัติการทำให้เกิดฟอง

efflo'rescence ← -flor- = ดอกไม้

• efflo'resce [v] = เบ่งบาน, ผลิดอกออกผล | ตกผลึก
• efflo'rescence [n] = ช่วงเวลาที่มีการผลิดอกออกผลมากที่สุด | ผื่นแดงบนผิวหนัง | สารผง ๆ บนผิวหน้า
• efflo'rescent [adj] = กำลังผลิดอก = abloom, flowering

eva'nescence ← evade, evite

• eva'nesce [v] = ค่อย ๆ จางหายไป
• eva'nescent [adj] = กำลังจะหายไป
• eva'nescence [n] = การ evanesce

ex'crescence ← excursive [adj] = ท่าทางจะหลุดประเด็น, (เนื้อหา) ครอบคลุมหลายเรื่อง

• ex'crescent [adj] = กำลังโตผิดปกติ
• ex'crescence [n] = สิ่งที่ยื่น/บวมออกมา | ส่วนของร่างกายที่โตผิดปกติ

flo'rescence ← -flor- = ดอกไม้

• flo'rescent [adj] = blossoming = efflorescent
• flo'rescence [n] = ช่วงเวลากำลังผลิดอก = efflorescence

fluo'rescence ← fluor [n] = CaF₂ (สามารถเปล่งแสงได้เมื่อโดน UV)

• fluo'rescent [adj] = เปล่งแสงได้
• fluo'rescence [n] = แสงที่มองเห็นได้ ซึ่งเกิดจากการดูดซับแสงที่ตามองไม่เห็น

inca'lescence ← -cal- = ความร้อน

• inca'lescent [adj] = กำลังร้อนขึ้น, ความร้อนกำลังเพิ่มขึ้น
• inca'lescence [n] = คุณสมบัติการรับความร้อน

incan'descence ← candent [adj] = เปล่งแสงเมื่อได้รับความร้อน

• incan'descent [adj] = candent | เร้าอารมณ์
• incan'descence [n] = การเปล่งแสงเมื่อได้รับความร้อน | แสงที่เกิดจาก incandescence

inflo'rescence ← -flor- = ดอกไม้

• inflo'rescence [n] = florescence | ส่วนที่เป็นดอก

infruc'tescence ← -fruct- = ผลไม้

• infruc'tescence [n] = ช่วงออกผล

intu'mescence ← tumor

• intumesce [v] = ลอยขึ้นเป็นฟอง (จากการให้ความร้อน) | ขยาย/โตอย่างผิดปกติ = swell, tumefy
• intumescent [adj] = swelling up, expanding
• intumescence [n] = การบวมเนื่องจากการอุดตันของของเหลว | การบวมเมื่อโดนความร้อน

iri'descence ← irised [adj] = มีหลากสี เหมือนรุ้ง

• iri'descent [adj] = มีสีต่างกัน เมื่อให้แสงต่างกัน หรือมองจากมุมต่างกัน | หลากสี
• iri'descence [n] = เปล่งแสงขาวนวลจาง ๆ

juve'nescence ← juvenile

• juvenile [n] = เด็ก
• juvenile [adj] = เด็ก
• juve'nescent [adj] = กำลัง (โตขึ้น) เป็นเด็ก
• juve'nescence [n] = การย่างเข้าสู่วัยเด็ก

lumi'nescence ← luminous [adj] = เปล่งแสง

• lumi'nescent [adj] = เปล่งแสงได้โดยไม่ต้องให้ความร้อน
• lumi'nescence [n] = การเปล่งแสงโดยไม่ต้องใช้ความร้อน | แสงจาก luminescence

obmu'tescence ← mute [adj] = เงียบ | พูดไม่ได้

• obmu'tescence [n] = การปิดปากเงียบ ไม่พูด

obso'lescence ← obso'lete

• obso'lesce [v] = become obsolete
• obso'lescent [adj] = becoming obsolete
• obso'lescence [n] = การ obsolesce

opa'lescence ← opal

• opa'lescent [adj] = iridescent
• opa'lescence [n] = iridescence

phospho'rescence ← phosphorus

• phospho'resce [v] = exhibit phosphorescence
• phospho'rescence [n] = phosphorescence

pu'bescence ← puberty

• pu'bescent [adj] = อยู่ในช่วงที่ต่อมสืบพันธุ์เริ่มทำงาน
• pu'bescence [n] = ช่วงที่ต่อมสืบพันธุ์เริ่มทำงาน

pu'trescence ← putrid, putrefaction

• putrid [adj] = เน่า, ส่งกลิ่นเหม็น
• putre'fy [v] = become putrid
• pu'trescent [adj] = becoming putrid
• pu'trescence [n] = การ putrefy | ช่วงเวลาที่กำลัง putrefy

qui'escence ← quiet

• qui'esce [v] = become quiet
• qui'escent [adj] = quiet, inactive
• qui'escence [n] = ความเงียบสงบ (อาจจะชั่วคราว)

recru'descence ← re'cur, re'cursion

• recru'desce [v] = เกิดขึ้น (อีกครั้ง), (แผล) เปิด
• recru'descent [adj] = recrudescing
• recru'descence [n] = การกลับคืนมา หลังจากหายไปหรือลดลง

rejuve'nescence ← re'juvenate, juvenile

• rejuve'nescent [adj] = becoming rejuvenated | causing to become rejuvenated
• rejuve'nescence [n] = การสร้างผนังเซลล์ใหม่ | การกลับไปเป็นเด็ก

se'nescence ← senior

• se'nesce [v] = grow old
• se'nescent [adj] = growing old
• se'nescence [v] = การแก่ตัวลง

tu'mescence ← tumor, tumid

• tumesce [v] = ขยาย/โต อย่างผิดปกติ = intumesce, swell, tumefy
• tu'mescent [adj] = บวม/โต อย่างผิดปกติ = tumid, turgid, swollen
• tu'mescence [n] = อาการบวมเนื่องจากการคั่งของของเหลว (เช่นเลือด) ในเนื้อเยื่อ = tumidity

Center of Mass & Centroid - ทฤษฎีบทของ Pappus

ทฤษฎีบทของ Pappus ที่กำลังจะบอกเนี่ย (คือ จริง ๆ เค้าคิดไว้หลายอัน) เป็นทฤษฎีพื้นฐานที่สำคัญมาก ในการหาปริมาณ n มิติของรูปเรขาคณิต เช่น ความยาว พื้นที่ ปริมาตร ฯลฯ เค้าบอกไว้ว่า ...

สมมติว่า เรามีเซต X ซึ่งอยู่ใน Rⁿ และมีปริมาณใน n มิติเท่ากับ A
แล้วเราเอา X ไปไว้ใน Rⁿ⁺¹

จับ X เคลื่อนที่ ในแนวตั้งฉากกับตัว X เอง เพื่อกวาดปริมาณใน n + 1 มิติ
บริเวณที่ X กวาดผ่าน จะมีปริมาณใน n + 1 มิติ เท่ากับ As
เมื่อ s = ระยะทางที่ centroid ของ X เคลื่อนที่

หวังว่า ไม่งงนะ :D

Direct Application

ดูตัวอย่างประกอบเลยละกัน ... อันนี้ค่อนข้างชัดเจนนะ

ดูทฤษฎีมันไม่ค่อยจะมีประโยชน์เลยเนอะ :P ... ลองดูอีกอันซิ

อันนี้ก็ ... ดูมีประโยชน์ขึ้นนิดนึงละ ... ไหนลองเอามาหาพื้นที่ผิวของรูป 3 มิติมั่งสิ

พื้นที่ผิวของกรวย ...

แล้วก็ เอามาหาปริมาตรมั่ง ... คราวนี้ X ต้องเป็น 2 มิตินะ

ตรงกับสูตร "(1/3) × ปริมาตรทรงกระบอก" เลย เห็นมั้ยว่า สูตรเรขาคณิตหลาย ๆ สูตร สามารถคิดได้ง่าย ๆ ด้วยทฤษฎีบทของ Pappus อันนี้

Reverse Use

เมื่อกี๊ ยกตัวอย่างไปแล้ว 4 ตัวอย่าง ทุกอันจะใช้ปริมาณใน n มิติ กับระยะการเคลื่อนที่ของ centroid เพื่อหาปริมาณใน n + 1 มิติ แต่จริง ๆ เราจะใช้กลับกันก็ได้ คือ ใช้หาตำแหน่ง centroid แทน

ตัวอย่างเช่น เรารู้อยู่แล้วว่า

ส่วนโค้งครึ่งวงกลม มีความยาว = πr
พื้นที่ผิวของทรงกลม = 4πr²

เราจะสามารถหา centroid ของส่วนโค้งครึ่งวงกลม ได้แบบนี้ ...

เอาตัวอย่างให้ดูอีกอันละกัน

พื้นที่ของครึ่งวงกลม = (1/2)πr²
ปริมาตรของทรงกลม = (4/3)πr³

เราจะหา centroid ของแผ่นครึ่งวงกลม ได้แบบนี้

จริง ๆ ที่เอาเรื่องนี้มาให้ดูเนี่ย เน้นที่ แนวการใช้กลับทางหนะ ... คือ ... อยากให้สังเกตกันว่า เมื่อเราคิดสมการอะไรได้ มันก็อาจจะมีวิธีใช้ในทางย้อนกลับ ซึ่งช่วยให้เราแก้ปัญหาบางอย่าง ได้ง่ายกว่าการคิดตรง ๆ

แนวคิดย้อนกลับ ก่อนนี้ก็เคยเอามาให้ดูไปแล้วเต็ม ๆ คือ ในเรื่อง ตามหาความหมายของ Determinant: Reverse Use - Height กับ ตามหาความหมายของ Determinant: Kramer's Rule นะ

Discrete vs Continuous: Taylor Series และ Newton Polynomial

Taylor Series

สมมติว่า เรามีฟังก์ชัน f ซึ่งต่อเนื่อง และมีอนุพันธ์ทุกอันดับที่ x₀

เราก็จะรู้ค่า f(x₀) f'(x₀) f''(x₀) ... ไปเรื่อย ๆ

คราวนี้ ถ้าเราอยากจะหาฟังก์ชัน f(x) ในรูปของพหุนาม เราจะใช้สมการนี้

f(x) = Σ_n≥0 f⁽ⁿ⁾(x₀)(x - x₀)ⁿ/n!

อนุกรมทางด้านขวาของสมการ เราเรียกว่า อนุกรมเทย์เลอร์ (Taylor Series)

ทำไมอนุกรมเทย์เลอร์ เท่ากับ f(x)?

เริ่มต้นเนี่ย เราก็สมมติว่า

f(x) = Σ_n≥0 a_n (x - x₀)ⁿ

แล้วหาค่า a_n ทุกตัว

พอเราแทนค่า x = x₀ เข้าไป จะเห็นว่า f(x₀) = a₀

เมื่อเราหาอนุพันธ์ทั้งสองข้าง เราจะได้ว่า

f'(x) = Σ_n≥1 na_n (x - x₀)^{n - 1}
= Σ_n≥0 (n + 1) a_n+1 (x - x₀)ⁿ

ซึ่งทำให้ f'(x₀) = a₁

หาอนุพันธ์อีกที จะได้

f''(x) = Σ_n≥1 n(n + 1) a_n (x - x₀)^{n - 1}
= Σ_n≥0 (n + 1)(n + 2) a_n+1 (x - x₀)ⁿ

ซึ่งทำให้ f''(x₀) = 2a₂

ทำไปเรื่อย ๆ เราจะสรุปได้ว่า

f⁽ⁿ⁾(x₀) = n! a_n
a_n = f⁽ⁿ⁾(x₀) / n!

ดังนั้น

f(x) = Σ_n≥0 f⁽ⁿ⁾(x₀)(x - x₀)ⁿ/n!

Newton Polynomial

ถ้าเรารู้ค่า f(x₀) Δf(x₀) Δ²f(x₀) ...

เราจะสามารถหาฟังก์ชัน f(x) ในรูปของพหุนามได้โดยสมการนี้

f(x) = Σ_n≥0 Δⁿf(x₀) (x - x₀)ⁿ/n!

เราเรียกสมการนี้ว่า สูตรผลต่างล่วงหน้าของนิวตัน (Newton's Forward Difference Formula)

วิธีพิสูจน์สูตรนี้ ก็ทำเหมือนเมื่อกี๊แหละ คือเราจะหาค่าของ Δⁿf(x₀) แต่ละตัวได้โดยการหาผลต่าง คือ

สมมติให้ f(x) = Σ_n≥0 a_n(x - x₀)ⁿ

เราก็จะหาค่า a_n ต่าง ๆ ได้ด้วยวิธีเหมือน ๆ กันกับกรณีของอนุกรมเทย์เลอร์ แบบนี้...

f(x₀) = a₀
Δf(x₀) = a₁
Δ²f(x₀) = 2a₂
...
Δⁿf(x₀) = n! a_n

ดังนั้น

a_n = Δⁿf(x₀) / n!

ซึ่งเมื่อแทนค่าลงไปในสมการที่เราตั้งขึ้น ก็จะได้สูตรนี้

f(x) = Σ_n≥0 Δⁿf(x₀) (x - x₀)ⁿ/n!

Abstraction

เราจะเห็นว่า การพิสูจน์สูตรทั้งสอง มีขั้นตอนที่เหมือนกันทุกประการ แต่มีการกำหนดสูตรเริ่มต้นที่ต่างกัน ซึ่งทำให้ การแปลง ที่ใช้ในการหาสัมประสิทธิ์ aⁿ ต้องเป็นคนละตัวกัน

ถ้าจะมองขั้นตอนทั้งหมด ให้เป็นกรณีทั่วไปมากขึ้น เราก็จะทำได้ดังนี้ ...

สมมติว่า มีการแปลงเชิงเส้น T และฟังก์ชัน s_n(x) ซึ่งมีคุณสมบัติดังนี้

s₀(0) = k
s_n(0) = 0 ; n > 0
Ts₀(x) = 0
Ts_n(x) = c_n s_n-1(x) ; n > 0
โดยที่ c_n ไม่เป็นฟังก์ชันของ x

เราจะสามารถสมมติฟังก์ชัน f(x) ให้เป็นแบบนี้ได้

f(x) = Σ_n≥0 a_n s_n(x)

เพราะ เมื่อเราแทนค่า x = 0 ลงไป เราจะหาค่า a₀ ได้ ...

f(0) = k a₀

ส่วนค่า a_n ตัวอื่น ๆ ก็สามารถหาได้โดยการใส่ T เข้าไปทั้งสองข้างของสมการที่เราสมมติขึ้น

Tf(x) = Σ_n≥0 a_n Ts_n(x)
Tf(x) = a₀Ts₀(x) + Σ_n≥1 a_n Ts_n(x)
Tf(x) = 0 + Σ_n≥1 a_n c_n s_n-1(x)
Tf(x) = Σ_n≥0 a_n+1 c_n+1 s_n(x)

พอเราแทนค่า x = 0 ก็จะได้ว่า

Tf(0) = a₁c₁k
a₁ = Tf(0) / c₁k

ส่วนค่า a₂ ก็จะหาได้โดยการใส่ T เข้าไปอีกที ที่สมการ Tf(x) = Σ_n≥0 a_n+1 c_n+1 s_n(x) จะได้ว่า

T²f(x) = Σ_n≥0 a_n+1 c_n+1 Ts_n(x)
T²f(x) = a₁c₁Ts₀(x) + Σ_n≥1 a_n+1 c_n+1 Ts_n(x)
T²f(x) = 0 + Σ_n≥1 a_n+1 c_n+1 c_n s_n-1(x)
T²f(x) = Σ_n≥0 a_n+2 c_n+2 c_n+1 s_n(x)

T²f(0) = a₂c₂c₁k
a₂ = T²f(0) / c₁c₂k

สังเกตดู จะเห็นว่า ถ้าทำไปเรื่อย ๆ เราก็จะหาค่า a_n ได้ทุกค่า ดังนี้

a_n = Tⁿf(0) / c₁c₂c₃...c_nk

ถ้ากำหนดให้ c₀ = k และเขียนผลคูณของ c_i ต่าง ๆ ด้วยเครื่องหมาย Π ก็จะได้ว่า

a_n = Tⁿf(0) / C(n)

เมื่อ C(n) = Π_0≤i≤n c_i

สรุปก็คือ

f(x) = Σ_n≥0 Tⁿf(0) s_n(x) / C(n)

กรณีของอนุกรมเทย์เลอร์

s_n(x) = xⁿ
T = d/dx
c₀ = 1
c_n = n ; n ≥ 1
C(n) = n!

กรณีของพหุนามนิวตัน

s_n(x) = xⁿ
T = Δ
c₀ = 1
c_n = n ; n ≥ 1
C(n) = n!

Transformation: Linear Transformation

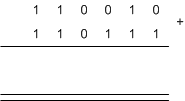
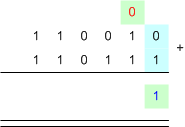
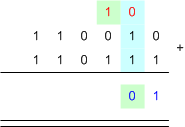
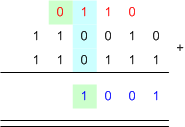
ปริภูมิเวกเตอร์ (Vector Space)

ปริภูมิเวกเตอร์ จะถูกนิยามด้วย 6 สิ่ง คือ

• เซตของเวกเตอร์ V
• การบวกของเวกเตอร์ +_V
• การคูณเวกเตอร์ด้วยสัมประสิทธ์ *_V
  
• เซตของสัมประสิทธิ์ F
• การบวกของสัมประสิทธ์ +_F
• การคูณของสัมประสิทธ์ *_F

โดยที่ (F, +_F, *_F) มีคุณสมบัติเป็น ฟิลด์ (Field) คือ

• ถ้า x, y ∈ F แล้ว x +_F y ∈ F และ x *_F y ∈ F
• ถ้า x, y, z ∈ F แล้ว x +_F (y +_F z) = (x +_F y) +_F z และ x *_F (y *_F z) = (x *_F y) *_F z
• ถ้า x, y ∈ F แล้ว x +_F y = y +_F x และ x *_F y = y *_F x
• มีสมาชิก 0_F ∈ F เพียงตัวเดียว ที่ทำให้ x +_F 0_F = x
• มีสมาชิก 1_F ∈ F เพียงตัวเดียว ที่ทำให้ x *_F 1_F = x
• ถ้า x ∈ F แล้ว จะมี (-x) ∈ F เพียงตัวเดียว ที่ทำให้ x +_F (-x) = 0_F
• ถ้า x ∈ F - { 0_F } แล้ว จะมี (1/x) ∈ F เพียงตัวเดียว ที่ทำให้ x *_F (1/x) = 1_F

และเงื่อนไขต่อไปนี้ เป็นจริง

• ถ้า x, y ∈ V และ c ∈ F แล้ว x +_V y ∈ V และ c *_V x ∈ V
• ถ้า x, y, z ∈ V แล้ว x +_V (y +_V z) = (x +_V y) +_V z
• ถ้า x, y ∈ V แล้ว x +_V y = y +_V x
• มีสมาชิก 0_V ∈ V เพียงตัวเดียว ที่ทำให้ x +_V 0_V = x
• ถ้า x ∈ V แล้ว จะมี (-x) ∈ V เพียงตัวเดียว ที่ทำให้ x +_V (-x) = 0_V
• ถ้า x ∈ V และ a, b ∈ F แล้ว a *_V (b *_V x) = (a *_F b) *_V x
• ถ้า x ∈ V แล้ว 1_F *_V x = x
• ถ้า x, y ∈ V และ c ∈ F แล้ว c *_V (x +_V y) = (c *_V x) +_V (c *_V y)
• ถ้า x ∈ V และ a, b ∈ F แล้ว (a +_F b) *_V x = (a *_V x) +_V (b *_V x)

ความนิยม

• เนื่องจาก การคูณและบวกที่ห้อย V กับ F จะทำได้เฉพาะกับสมาชิกที่มาจากเซตต่างกัน เราสามารถตัดตัวห้อยทิ้ง แล้วก็ยังเข้าใจถูกต้องอยู่
• เราสามารถตัดเครื่องหมายการคูณทิ้งได้ด้วย โดยใช้การเขียนติดกันแทน
• 0_V เราจะใช้ตัวหนาเขียนแทน เป็น 0 เพื่อให้ สามารถเขียน 0 และ 1 แทน 0_F และ 1_F ได้ ตามลำดับ
• เขียนแทน a + (-b) ด้วย a - b เพื่อให้สั้นลง
• เขียนแทน a(1/b) ด้วย a/b เพื่อให้สั้นลง
• เมื่อไม่เขียนวงเล็บ ให้คิดการคูณก่อนการบวก และคิดจากซ้ายไปขวาเสมอ
• ตัวแปรที่เป็นสมาชิกของ V จะเขียนด้วยตัวหนา
  

การแปลงเชิงเส้น (Linear Transformation)

ถ้า f:V → W เป็นการแปลงเชิงเส้น (Linear Transformation) และ V กับ W เป็น ปริภูมิเวกเตอร์ ซึ่งมีฟิลด์ของสัมประสิทธิ์เดียวกันคือ F

• สำหรับ x ∈ A และ y ∈ A ทุกตัว: f(x + y) = f(x) + f(y) ∈ B
  
• สำหรับ x ∈ A และ c ∈ F: f(cx) = cf(x) ∈ B
  

สิ่งที่รู้ทันที คือ

f(0_V) = 0_W

เราก็เลย เขียนว่า 0 เฉย ๆ ได้ พิสูจน์ได้ ไม่ยากหรอก

Kernel และ Image

เมื่อไหร่ที่เราพูดถึง homomorphism (และ linear transformation) จะต้องมีคำศัพท์ที่เรายุ่งด้วย 2 คำ คือ Kernel และ Image เสมอ ๆ

kernel ของ f = { x ∈ V | f(x) = 0 }
image ของ f = { f(x) | x ∈ V }

ความจริงที่สิ่งสำคัญมาก ๆ อย่างนึงก็คือ kernel ของ f เป็น ปริภูมิเวกเตอร์ย่อย (Vector Subspace) ของ V ซึ่งก็คือ ถ้าเราเอา kernel ของ f ไปใส่แทน V ในเงื่อนไขต่าง ๆ ของปริภูมิเวกเตอร์ ที่เขียนไว้ข้างบน มันก็จะเป็นจริงทั้งหมดเช่นกัน

ตัวอย่าง: ให้ K = kernel ของ f

x, y ∈ K ⇒ f(x) = f(y) = 0
ดังนั้น f(x + y) = 0 + 0 = 0
แสดงว่า x + y ∈ K ด้วย

เงื่อนไขอื่น ๆ ก็พิสูจน์ได้ด้วยวิธีคล้าย ๆ กัน

Quotient Subspaces

เนื่องจาก ปริภูมิเวกเตอร์ มีคุณสมบัติการสลับที่การบวก ดังนั้น เราอาจจะมองว่า (V, +) เป็น กรุปอาบีเลียน (Abelian Group) ซึ่ง คุณสมบัตินี้ ทำให้ กรุปย่อย (Subgroup) ทุกอันของ V เป็น กรุปย่อยปกติ (Normal Subgroup) ด้วย (ใครอ่านอันนี้ไม่รู้เรื่อง ช่างมันไปก่อน)

ผลก็คือ เราจะสามารถหา coset (ไม่ต้องไปสนชื่อมันก็ได้) ต่อไปนี้ได้

q(x) = { k + x | k ∈ K }
เมื่อ x ∈ V

เพื่อความสะดวก เราจะเขียนแทน q(x) ด้วยสัญลักษณ์นี้

q(x) = K + x

คราวนี้ ถ้าเรานิยามการบวกและคูณ สำหรับ q(x) ต่าง ๆ ใหม่ แบบนี้

(K + x) + (K + y) = K + (x + y)
c(K + x) = K + cx

และให้เอกลักษณ์ของการบวก คือ

K + 0 = 0_K = K

เราจะพิสูจน์ได้ว่า เซตของ q(x) และเครื่องหมายบวกกับคูณแบบใหม่นี้ ก็เป็นปริภูมิเวกเตอร์เช่นกัน เรามักจะเขียนเซตของ q(x) ทั้งหมด ว่า V/K

Isomorphisms

Isomorphism ของ ปริภูมิเวกเตอร์ ก็คือ การแปลงเชิงเส้นที่มีคุณสมบัติ 1-1 และทั่วถึงน่ะแหละ

ปริภูมิเวกเตอร์ A และ B จะ Isomorphic กัน ก็ต่อเมื่อ มี isomorphism จาก A ไป B

ที่อยากจะบอกก็คือ V/K เนี่ย isomorphic กับ image ของ f นะ

พิสูจน์ยังไงน่ะหรอ? เราก็สร้าง isomorphism φ ขึ้นมาอันนึง แบบนี้

φ(K + x) = f(x)

คราวนี้ เราจะบอกว่า φ มันมีคุณสมบัติ 1-1 ได้โดย

สมมติว่า φ(K + x) = φ(K + y)
แสดงว่า f(x) = f(y)
ซึ่งทำให้ f(x) - f(y) = 0
f(x - y) = 0 = φ(K + (x - y))
แต่จากนิยามของ K เมื่อ f(x - y) = 0 แสดงว่า x - y ∈ K = 0_K
ทำให้ K + (x - y) = 0_K
(K + x) - (K + y) = 0_K
K + x = K + y

การพิสูจน์ว่า φ มีคุณสมบัติทั่วถึง จะง่ายกว่า คือทำแบบนี้

สมมติว่า y ∈ image ของ f
เราจะรู้ว่า ต้องมี x ∈ V ที่ทำให้ f(x) = y
ดังนั้น K + x ∈ V/K จะทำให้ φ(K + x) = y แน่นอน

คุณสมบัติอื่น ๆ ไม่พูดถึงแล้วนะ ไปพิสูจน์กันเอาเอง

Cardinal Numbers

สมมติว่า W = image ของ f เราจะรู้สิ่งที่สำคัญมาก ๆ ก็คือ

|V| = |K| × |W| = |K| × |V/K|

เมื่อ | ... | หมายถึง cardinal number

Dimensions

ใครที่เรียน linear algebra คงพอจะรู้ว่า dimension คืออะไรนะ

ยกตัวอย่างคร่าว ๆ ละกัน

dim R = 1
dim R² = 2
dim R³ = 3
...
dim Rⁿ = n

dim span( { (1, 1), (1, 0) } ) = 2
dim span( { (1, 1, 1), (1, 1, 0), (1, 0, 0) } ) = 3
dim span( { (1, 1, 1), (1, 1, 0), (0, 0, 1) } = 2
dim span( { (1, 1, 1), (2, 2, 2), (3, 3, 3) } = 1

จะว่าไป dimension มันก็ คล้าย ๆ กับ เอาขนาดของเซต ใส่ log ฐาน c = |R| เลย ... เราก็เลยได้ความสัมพันธ์คล้าย ๆ กัน แบบนี้

จาก |V| = |K| × |W|

ใส่ log_c เมื่อ c = |R| เข้าไปทั้งสองข้าง จะได้

log_c|V| = log_c(|K| × |W|)
log_c|V| = log_c|K| + log_c|W|

dim V = dim K + dim W

พับกล่องลูกบาศก์

เวลาเราจะพับกล่องลูกบาศก์ด้วยกระดาษเนี่ย รู้สึกเหมือน ตอนเด็ก ๆ เค้าจะบอกให้ตัดกระดาษมาแบบนี้

แต่จริง ๆ แล้วมันตัดแบบอื่นก็ได้นะ ... คือ ถ้าเราเอาเส้นตรง 4 ช่อง มาม้วน มันจะได้กล่องที่แหว่งไป 2 ด้าน ซึ่งทั้งสองด้านนั้น อยู่ตรงข้ามกัน เราสามารถเพิ่มด้านที่หายไปได้ โดยเอาไปติดกับขอบใดขอบนึง ...

ดังนั้น รูปของกระดาษที่ทำเป็นกล่องได้ จะสามารถคิดได้แบบนี้

รูปทั้งหมดที่เป็นไปได้ก็คือ

(ไปหมุน ๆ สลับ ๆ เอาเองนะ)

รูปต่อไปนี้ คือรูปที่มีเส้นแนวกลางยาว 3 และพับเป็นกล่องได้

แต่นอกจากรูปพวกนี้ ก็ยังมีอีก 2 แบบ ที่พับเป็นกล่องได้ คือ

วิธีคิดอย่างหยาบ ๆ ว่า รูปไหนสามารถทำได้บ้าง เราคิดแบบนี้

"หน้าแต่ละหน้า จะมีหน้าตรงข้ามได้เพียงหน้าเดียว"

สมมติว่า เราต้องการหาหน้าที่อยู่ตรงข้ามกับหน้า X เราจะใช้หลักการแบบนี้

ถ้ามีแผ่นที่อยู่ติดกับ X ด้านบน แผ่นที่อยู่เหนือ X 2 ช่องที่อยู่ใกล้กับ X มากที่สุด จะเป็นหน้าตรงข้ามของ X

เช่น ในรูปข้างล่างนี้ แผ่นสีฟ้ากับเขียว จะเป็นหน้าตรงข้ามกัน

ในทิศอื่น ๆ เราก็คิดแบบนี้เหมือนกัน

ลองเอารูปที่ทำได้ซักอันนึง มาวิเคราะห์ดูสิ

เมื่อเราวิเคราะห์รูปที่ไม่สามารถพับเป็นกล่องได้ เราจะพบว่า หน้าบางหน้าไม่มีหน้าตรงข้าม หรือ หน้าบางหน้ามีหน้าตรงข้ามมากกว่า 1

ในรูปข้างล่างนี่ หน้าสีแดง ไม่มีหน้าตรงข้าม

ส่วนในรูปข้างล่างนี้ หน้าสีฟ้า มีหน้าตรงข้ามมากกว่า 1

จบละ :D

การยกกำลังกับจำนวนเชิงซ้อน

ก่อนเริ่ม

จำนวนเชิงซ้อนใด ๆ สามารถเขียนในรูป

a + ib และ re^iθ

ได้ โดยที่ค่า a b r และ θ เป็นจำนวนจริง

ค่า θ สามารถมีได้หลายค่า เพราะว่า

e^iθ = cos θ + i sin θ

ดังนั้น

e^iθ = e^{i(θ + 2πn)}

สำหรับจำนวนเต็ม n ใด ๆ

ต่อไปนี้ จะให้ y กับ z เป็นจำนวนเชิงซ้อน ซึ่ง y = a + ib และ z = re^iθ และ x เป็นจำนวนจริงนะ

การยกกำลังจำนวนจริงด้วยจำนวนเชิงซ้อน

x^y = x^{a + ib} = x^a x^ib = x^a (e^{ln x})^ib = x^a e^{ib ln x}

ถ้าให้ x > 0 แล้ว f(a, b) = x^a e^{ib ln x} เป็นฟังก์ชัน 1 ต่อ 1 รึเปล่า?

คำตอบก็คือ "ไม่" ...

เหตุผลแรก ... ถ้า x = 1 เราจะเห็นว่า x^a = 1 เสมอ ไม่ว่า a จะเป็นอะไร ดังนั้น f(a, b) จะเท่ากันสำหรับทุกค่า a

แล้วถ้าเพิ่มเงื่อนไขให้เป็น x ∈ R⁺ - { 1 } หละ?

ก็ยังไม่ได้อยู่ดี เพราะว่า e^{ib ln x} = e^{i(b ln x + 2πn)} ดังนั้น

ถ้าให้ b' ln x = b ln x + 2πn
b' = b + 2πn / ln x
e^{ib ln x} = e^{ib' ln x}

จะเห็นว่า สามารถทำให้ f(a, b') = f(a, b) ได้โดยที่ b' ≠ b

งั้น ... ถ้าเราเพิ่มอีกเงื่อนไขนึง คือ b ln x ∈ [0, 2π) หละ?

f(a, b) ก็จะเป็นฟังก์ชัน 1 ต่อ 1 แล้ว!

การยกกำลังจำนวนเชิงซ้อนด้วยจำนวนจริง

z^x = (re^iθ)^x = r^xe^iθx

f(x) = z^x อาจจะไม่เป็นฟังก์ชันนะ!

ทำไมน่ะเหรอ? ... ก็ เพราะว่า e^iθ = e^{i(θ + 2πn)} หนิ ลองเอาไปแทนใหม่ดู

f(x) = z^x = (re^{i(θ + 2πn)})^x = r^xe^{i(θx + 2πnx)}

พอเป็นหยั่งงี้ มันก็เริ่มดูเพี้ยน ๆ แล้วหละ ... z^x มีได้หลายค่า ขึ้นอยู่กับ n ... f(x) ไม่ใช่ฟังก์ชันแล้ว!

จริง ๆ มันก็ไม่แปลกเท่าไหร่นะ ... ก็ ตอนเราหาคำตอบของสมการ z² = 1 เรายังได้คำตอบ 2 ค่าเลยหนิ

แล้วเมื่อไหร่ f(x) จะเป็นฟังก์ชันหละ?

• ถ้า x เป็นจำนวนเต็ม → nx เป็นจำนวนเต็ม
• พอ nx เป็นจำนวนเต็มแล้ว → g(x) = e^{i(θx + 2πnx)} มีได้ค่าเดียว ก็เลยเป็นฟังก์ชัน
• เนื่องจาก f(x) = r^xg(x) และ g(x) เป็นฟังก์ชัน → f(x) เป็นฟังก์ชัน

นี่ก็แปลว่า ถ้าให้ x เป็นจำนวนเต็ม z^x จะเป็นฟังก์ชัน นั่นเอง

แต่ เพื่อให้เขียนสะดวก เรามักจะสมมติให้ z^x เป็นฟังก์ชัน โดยเพิ่มข้อกำหนดอีกแบบเข้าไปเลย คือ

z = re^iθ เมื่อ 0 ≤ θ < 2π
และ z^x = r^xe^ixθ

ค่าของ iⁱ

เนื่องจาก i = e^iπ/2 ดังนั้น

iⁱ = (e^iπ/2)ⁱ = e^-π/2

อ๊ะ ... iⁱ = e^-π/2 = 0.207879576... !!!

ไม่ใช่ิสิ :P ... อย่าลืมว่า จริง ๆ แล้ว i = e^{i(π/2 + 2πn)} เมื่อ n เป็นจำนวนเต็มบวกใด ๆ ... คิดใหม่แบบติด n ก็จะได้

iⁱ = (e^{i(π/2 + 2πn)})ⁱ = e^{-π/2 - 2πn}

iⁱ ก็เลยมีได้หลายค่า ... แต่ทุกค่า เป็นจำนวนจริงนะ!

การยกกำลังจำนวนเชิงซ้อนด้วยจำนวนเชิงซ้อน

คราวนี้ มาลองหาค่า z^y กัน ...

z^y = (re^iθ)^{a + ib} = [r^a r^ib] (e^iθ)^{a + ib}
z^y = [r^a e^{ib ln r}] (e^{i(θ + 2πm)})^{a + ib}
z^y = r^a e^{i(b ln r + 2πn)} e^{i(θa + 2πma)} e^{-θb - 2πmb}
z^y = [r^ae^{-θb - 2πmb}] e^{i(b ln r + θa + 2πma + 2πn)}

จะเห็นว่า ค่าของ z^y จะมีได้หลายค่า อยากที่คาดเอาไว้ แต่คราวนี้ มีตัวแปรอิสระถึง 2 ตัว คือ m กับ n

ดังนั้น ถ้าเป็นไปได้ ก็ไม่ควรเอาจำนวนเชิงซ้อนมายกกำลังกันนะ :D