Center of Mass & Centroid - ทฤษฎีบทของ Pappus

ทฤษฎีบทของ Pappus ที่กำลังจะบอกเนี่ย (คือ จริง ๆ เค้าคิดไว้หลายอัน) เป็นทฤษฎีพื้นฐานที่สำคัญมาก ในการหาปริมาณ n มิติของรูปเรขาคณิต เช่น ความยาว พื้นที่ ปริมาตร ฯลฯ เค้าบอกไว้ว่า ...

สมมติว่า เรามีเซต X ซึ่งอยู่ใน Rⁿ และมีปริมาณใน n มิติเท่ากับ A
แล้วเราเอา X ไปไว้ใน Rⁿ⁺¹

จับ X เคลื่อนที่ ในแนวตั้งฉากกับตัว X เอง เพื่อกวาดปริมาณใน n + 1 มิติ
บริเวณที่ X กวาดผ่าน จะมีปริมาณใน n + 1 มิติ เท่ากับ As
เมื่อ s = ระยะทางที่ centroid ของ X เคลื่อนที่

หวังว่า ไม่งงนะ :D

Direct Application

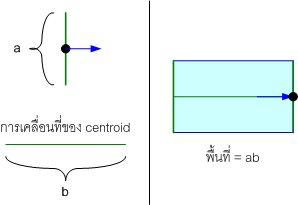
ดูตัวอย่างประกอบเลยละกัน ... อันนี้ค่อนข้างชัดเจนนะ

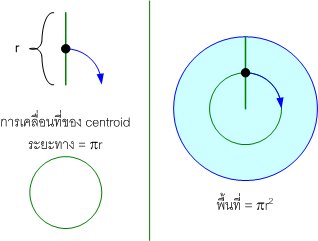
ดูทฤษฎีมันไม่ค่อยจะมีประโยชน์เลยเนอะ :P ... ลองดูอีกอันซิ

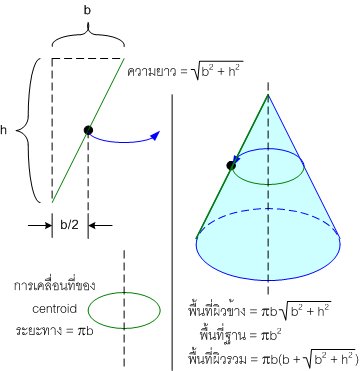
อันนี้ก็ ... ดูมีประโยชน์ขึ้นนิดนึงละ ... ไหนลองเอามาหาพื้นที่ผิวของรูป 3 มิติมั่งสิ

พื้นที่ผิวของกรวย ...

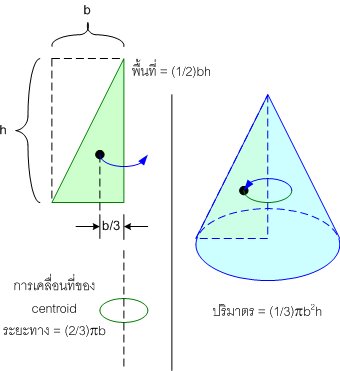
แล้วก็ เอามาหาปริมาตรมั่ง ... คราวนี้ X ต้องเป็น 2 มิตินะ

ตรงกับสูตร "(1/3) × ปริมาตรทรงกระบอก" เลย เห็นมั้ยว่า สูตรเรขาคณิตหลาย ๆ สูตร สามารถคิดได้ง่าย ๆ ด้วยทฤษฎีบทของ Pappus อันนี้

Reverse Use

เมื่อกี๊ ยกตัวอย่างไปแล้ว 4 ตัวอย่าง ทุกอันจะใช้ปริมาณใน n มิติ กับระยะการเคลื่อนที่ของ centroid เพื่อหาปริมาณใน n + 1 มิติ แต่จริง ๆ เราจะใช้กลับกันก็ได้ คือ ใช้หาตำแหน่ง centroid แทน

ตัวอย่างเช่น เรารู้อยู่แล้วว่า

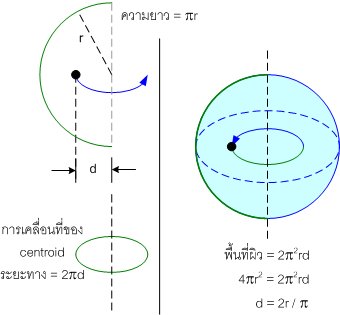
ส่วนโค้งครึ่งวงกลม มีความยาว = πr
พื้นที่ผิวของทรงกลม = 4πr²

เราจะสามารถหา centroid ของส่วนโค้งครึ่งวงกลม ได้แบบนี้ ...

เอาตัวอย่างให้ดูอีกอันละกัน

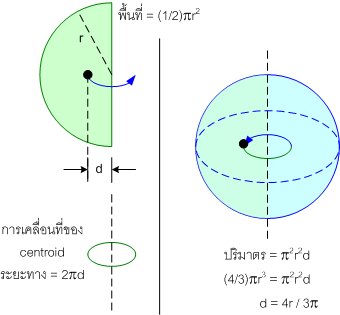
พื้นที่ของครึ่งวงกลม = (1/2)πr²
ปริมาตรของทรงกลม = (4/3)πr³

เราจะหา centroid ของแผ่นครึ่งวงกลม ได้แบบนี้

จริง ๆ ที่เอาเรื่องนี้มาให้ดูเนี่ย เน้นที่ แนวการใช้กลับทางหนะ ... คือ ... อยากให้สังเกตกันว่า เมื่อเราคิดสมการอะไรได้ มันก็อาจจะมีวิธีใช้ในทางย้อนกลับ ซึ่งช่วยให้เราแก้ปัญหาบางอย่าง ได้ง่ายกว่าการคิดตรง ๆ

แนวคิดย้อนกลับ ก่อนนี้ก็เคยเอามาให้ดูไปแล้วเต็ม ๆ คือ ในเรื่อง ตามหาความหมายของ Determinant: Reverse Use - Height กับ ตามหาความหมายของ Determinant: Kramer's Rule นะ