Transformation Matrix: ผลคูณภายใน

เรื่องนี้เป็นภาคต่อของ Transformation Matrix: พื้นฐาน นะ ไม่ยากเหมือนตอนที่แล้ว ๆ มา

เราจะเริ่มที่เรื่องของ ผลคูณภายใน ก่อน แต่คราวนี้ จะคิดกรณีของจำนวนเชิงซ้อนด้วย

สมมติว่าเรามีเวกเตอร์ u อยู่ เราคิดว่า ค่าในแต่ละมิติของ u เป็นฟังก์ชันของเลขมิติ (เหมือนกับในตอน Discrete: ฟังก์ชัน เวกเตอร์ และเมตริกซ์) คือ

u = (u(1), u(2), u(3), ..., u(n))

แต่เดิม เราคิดว่าผลคูณภายในของ u กับ v ที่มีมิติเป็น n เท่ากัน คือ

u ⋅ v = Σ_1≤i≤n u(i)v(i)

ดังนั้น ขนาดของ u สามารถหาได้จาก (คราวนี้ขอเขียนว่า |u| นะ)

|u|² = u ⋅ u = Σ_1≤i≤n u(i)²

หรือก็คือ

|u| = (u ⋅ u)^1/2

แต่ ถ้าเกิด u(i) เป็นจำนวนเชิงซ้อนหละ ... u ⋅ u อาจจะไม่ใช่จำนวนจริงก็ได้ แล้ว |u| ก็อาจจะมีได้ 2 ค่าน่ะสิ (จากสมการ |u|² = u ⋅ u)

เราแก้ปัญหานี้ได้ โดยนิยามอะไรใหม่นิดนึง ... ถ้าเรากำหนดให้ สังยุกต์ (Conjugate) ของเวกเตอร์ เป็นแบบนี้

u^* = (u(1)^*, u(2)^*, u(3)^*, ..., u(n)^*)

พอเราหา u^* ⋅ u ผลก็คือ

u^* ⋅ u = Σ_1≤i≤n u(i)^*u(i)

จากความรู้เรื่องจำนวนเชิงซ้อน เรารู้ว่า ถ้า z เป็นจำนวนเชิงซ้อนใด ๆ แล้ว z^*z = |z|² เป็นจำนวนจริง ดังนั้น u^* ⋅ u ของเรา ก็จะเป็นจำนวนจริงด้วย

เราเลยนิยาม ผลคูณภายใน ใหม่ แบบนี้

u ⋅ v แบบใหม่ = u^* ⋅ v แบบเก่า

แต่ u ⋅ v แบบใหม่ มีคุณสมบัติต่างกับแบบเก่าด้วย คือ

u ⋅ v ≠ v ⋅ u (หมายถึง ไม่จำเป็นต้องเท่ากันเสมอไป)
แต่ u ⋅ v = (v ⋅ u)^* เสมอ

เมื่อคิดเวกเตอร์เป็นเมตริกซ์แนวตั้ง

ถ้าเรามอง u เป็นเมตริกซ์มิติ n × 1 เราก็ยังเขียนว่า

u = (u(1), u(2), u(3), ..., u(n))

ได้เหมือนเดิม ... แต่เดี๋ยวลองกำหนด u^* ใหม่ ให้เป็นแบบนี้

u^* = [u(1)^* u(2)^* u(3)^* ... u(n)^*]

หรือก็คือ

u^* แบบใหม่ = (u^*)^T แบบเก่า

พอเราหาผลคูณแบบเมตริกซ์ของ u^* กับ v ก็จะได้ผลเป็น เมตริกซ์มิติ 1 × 1 แบบนี้

u^*v = [u ⋅ v]

เพื่อให้เขียนง่ายขึ้น เราจะถือซะว่า เมตริกซ์มิติ 1 × 1 เป็นจำนวนเชิงซ้อนตัวเดียวเลยละกัน ... มันจะเป็น

u^*v = u ⋅ v

ผลคูณภายในของเมตริกซ์กับเมตริกซ์

เราลองใช้นิยามผลคูณภายในอย่างเดียวกันกับเมตริกซ์ดู เราจะหาขนาดของเมตริกซ์ได้รึเปล่านะ?

A ⋅ A = A^*A = ?

ถ้าเรามองว่า A เป็นเมตริกซ์ที่มีมิติ m × n ซึ่งประกอบด้วยเวกเตอร์แนวตั้ง แบบนี้

A = [A₁ : A₂ : A₃ : ... : A_m]

A^* จะเป็นเมตริกซ์ที่มีมิติ n × m หน้าตาแบบนี้

A^* = (A₁^* : A₂^* : A₃^* : ... : A_m^*)

เผื่อลืม: รูปการคูณเมตริกซ์

เอามาจาก Transformation Matrix: พื้นฐาน นะ

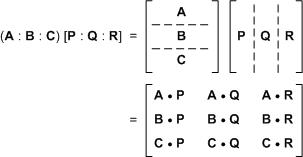
ดังนั้นค่าของ A^*A จะเป็นเมตริกซ์มิติ n × n แบบนี้

B = A^*A
B_i,j = A_i ⋅ A_j

เมื่อ B_i,j คือ ค่าในแถวที่ i หลักที่ j ของ B

คราวนี้ คุณสมบัติสำคัญก็คือ

A_i ⋅ A_j = (A_j ⋅ A_i)^*

ซึ่งทำให้

B_i,j = B_{j, i}^*

ซึ่งแปลว่า

B = B^*

เราเรียกเมตริกซ์ที่มีคุณสมบัตินี้ว่า เมตริกซ์เฮอร์มิเชียน (Hermitian Matrix)

ไป ๆ มา ๆ เราก็ไม่ได้ขนาดของ A แฮะ แต่ได้คุณสมบัติที่ว่า A ⋅ A เป็นเมตริกซ์เฮอร์มิเชียนแทน

แล้ว แต่ละค่า B_i,j มันมีความหมายว่ายังไงหละ?

ถ้าเวกเตอร์ A_i ตั้งฉากกันทุกคู่

ดังนั้น A_i ⋅ A_j จะเป็น 0 เมื่อ i ≠ j

มันก็แปลว่า B_i,j = 0 เมื่อ i ≠ j น่ะสิ

A ⋅ A ก็จะเป็น เมตริกซ์ทแยงมุม (Diagonal Matrix)!!!

เราจะเขียนได้ว่า ... (สัญลักษณ์แบบนี้ เอามาจาก Transformation Matrix: Eigenvalues & Eigenvectors "ตอนแรก" นะ)

A ⋅ A = [ B_1,1 \ B_2,2 \ B_3,3 \ ... \ B_n,n ]

เนื่องจาก B_i,i = A_i ⋅ A_i = |A_i|² เป็นจำนวนจริง ดังนั้น

A ⋅ A เป็นเมตริกซ์จำนวนจริงด้วย

เรื่องของ Determinant

ถ้า A เป็นเมตริกซ์จัตุรัส เราจะหา det(A) ได้

เนื่องจาก det(A) เกิดจากการเอาค่า A มาคูณกับบวกกัน ดังนั้น

det(A^*) = det(A)^*

ดังนั้น เราก็เลยรู้แน่ ๆ ว่า

det(A ⋅ A) เป็นจำนวนจริง

เพราะว่า

det(A ⋅ A) = det(A^*A) = det(A)^*det(A)

เป็นจำนวนจริงแน่นอน

ดังนั้น เราอาจจะนิยาม ขนาดของ A อีกแบบนึง ซึ่งเป็นจำนวนจริงไม่ติดลบเสมอ ดังนี้

|A| = det(A ⋅ A)^1/2

ซึ่งสิ่งที่เราได้เพิ่มมาอีกอย่างก็คือ ... A ไม่จำเป็นต้องเป็นเมตริกซ์จัตุรัสก็ได้น่ะสิ !!!