Discrete: ฟังก์ชัน เวกเตอร์ และเมตริกซ์

เรื่องนี้ ต่อเนื่องมาจาก Discrete: ผลคูณภายใน และ การถ่วงน้ำหนัก" นะ คราวนี้จะไม่มีอะไรหนัก ๆ เหนื่อย ๆ แต่ยาวอะ ต้องดูรายละเอียดให้ดี ๆ หน่อยนะ ... มันดูเหมือนไม่มีอะไร แต่ก็พอมีเหมือนกัน

เวกเตอร์ = ฟังก์ชัน

สมมติว่า u เป็นเวกเตอร์ใน n มิติ โดยที่

u = (u₁, u₂, u₃, ..., u_n)

เราอาจจะมองว่า u_x เป็นฟังก์ชันของ x ที่มีโดเมนเป็น {1, 2, 3, ..., n} ก็ได้

ดังนั้น ต่อจากนี้ไปจะเขียน u(x) แทน u_x นะ

สมมติว่า α เป็นเวกเตอร์ n มิติที่ค่าในทุกแกนเป็น 1 เราจะเขียนได้ว่า

α(x) = 1

คราวนี้ ผลคูณภายในของ α กับ u ก็จะมีหน้าตาเป็น...

α⋅u = Σ_1≤x≤n u(x)

กลายเป็นผลรวมของ u(x) ตั้งแต่ x = 1 ถึง n น่ะเอง

ขยายสัญลักษณ์เราอีกนิดนึง ... สมมติว่าโดเมนเราไม่ใช่ {1, 2, 3, ..., n} แต่เป็นเซตจำกัดอื่น ซึ่งมีจำนวนสมาชิกเท่ากัน สมมติให้ชื่อว่า D เราจะสามารถหาฟังก์ชันหนึ่งต่อหนึ่งและทั่วถึง T: {1, 2, 3, ..., n} → D ได้

เพื่อให้เขียนง่าย ๆ หน่อย เราก็นิยามซะเลยว่า

u⋅v = Σ_x∈D u(x)v(x)

เมื่อ D คือโดเมนร่วมของ u และ v

พอสัญลักษณ์เราเป็นแบบนี้แล้ว D ของเรา อาจจะเป็นเซตอนันต์ก็ได้นะ

เมตริกซ์ = ฟังก์ชันของเวกเตอร์ = ฟังก์ชันสองตัวแปร → ผลคูณของเมตริกซ์ = ผลคูณภายใน

สมมติว่า A = [ A₁ : A₂ : A₃ : ... : A_m ] เมื่อ A_x เป็นเวกเตอร์ n มิติ

คิดเหมือนกับเวกเตอร์ก็คือ เราจะมอง A_x เป็นฟังก์ชันของ x ก็ได้ ดังนั้นก็เขียนเป็น A(x) แทนละกัน แต่เนื่องจาก A(x) ก็เป็นเวกเตอร์อีก เราจะมองว่า (A(x))_y = A(x, y) ก็ได้อีก

สมมติว่า D = {1, 2, 3, ..., m} และ E = {1, 2, 3, ..., n} เราจะมอง A เป็นฟังก์ชันได้สองแบบ คือ

1. A: D → Rⁿ จะได้ว่า A(x) เป็นเวกเตอร์ n มิติ
2. A: D × E → R จะได้ว่า A(x, y) เป็นสเกลาร์

ถ้ามองแบบแรก เราจะสามารถหาผลคูณภายในของ A กับฟังก์ชันที่มีโดเมนเดียวกันคือ D ได้

สมมติว่า b = (b(1), b(2), b(3), ..., b(m))
ผลคูณภายในของ A กับ b ก็จะเป็น:

c = A ⋅ b = Σ_x∈D A(x) b(x)

ซึ่งถ้าคิดทีละตัวของผลลัพธ์ จะเห็นว่า

c(y) = Σ_x∈D A(x, y) b(x)

ซึ่งถ้าเรากำหนดให้ A'(y) = (A(1, y), A(2, y), A(3, y), ..., A(m, y)) ก็จะยุบรูปได้เป็น

c(y) = A'(y) ⋅ b

จากเรื่องในตอนเก่า ๆ (ดูอันบนก็พอ)

เห็นมั้ยว่า...

A ⋅ b = Ab เมื่อคูณแบบเมตริกซ์ !!!

รู้หยั่งงี้ ก็ไม่ต้องจำแล้ว ว่าคูณเมตริกซ์มันทำกันยังไง :D

ถ้างง ๆ ก็เอารูปนี้ไปลองเพ่ง ๆ ดูนะ (รูปในตอนเก่าหนะ) นี่เป็นกรณี 2 มิติที่ m = n น่าจะง่ายหน่อย แต่แนวคิดเดียวกัน จะเอาไปขยายให้ m กับ n เป็นเท่าไหร่ก็ได้

ข้างล่างนี่แหละ ผลลัพธ์ที่ต้องการ (ไม่ต้องสนใจตรงที่บอกว่า "= w" นะ)

เรื่องของคำศัพท์: การคูณ และ การแปลง

เคยสงสัยมั้ยว่า ทำไมบางทีเรียกเมตริกซ์ว่า "การแปลง"?

เหตุผลมันอยู่ในสมการข้างบน สองสมการนี่แหละ (ยกมาให้ดูตรงนี้อีกทีละกัน จะได้ไม่ต้องกลับขึ้นไปดู)

c = A ⋅ b = Σ_x∈D A(x) b(x)
c(y) = Σ_x∈D A(x, y) b(x)

แต่เดิมที b เป็นฟังก์ชันของ x (คือมีโดเมนเป็น D = {1, 2, 3, ..., n}) พอเอา A มาคูณข้างหน้า ได้ผลลัพธ์เป็น c ซึ่งเป็นฟังก์ชันของ y (คือมีโดเมนเป็น E = {1, 2, 3, ..., m}) นี่แหละถึงเรียก A ว่าเป็น "การแปลง" (Transformation)

ถ้าให้ A เป็นเมตริกซ์จัตุรัส เราอาจจะมองได้ง่ายขึ้นนิดหน่อย ... ลองดูรูปนี้ (รูปเก่าเล่าใหม่อีกแล้ว :P)

รูปนี้ก็คือ ถ้าเรามีจุด (a, b) อยู่ในระบบพิกัด u-v และเรารู้ค่าของ u กับ v เทียบกับ i และ j เราก็จะสามารถแปลง (a, b) ให้เป็น (x, y) ในพิกัด i-j ได้โดยเอา [ u : v ] มาคูณกับ (a, b)

ในกรณีนี้ [ u : v ] ก็คือเมตริกซ์การแปลงของเรา

อินเวอร์สของการแปลง... ก็อินเวอร์สเมตริกซ์น่ะแหละ

อันนี้ต่อเนื่องจากเมื่อกี๊เลย เรารู้ว่า [ u : v ] เป็นเมตริกซ์การแปลง ซึ่งใช้แปลง (a, b) เป็น w = (x, y) แต่นอกจากนี้ เรายังรู้อีกอย่างจากในตอน ตามหาความหมายของ Determinant: Kramer's Rule ก็คือ

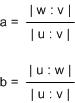
ซึ่งแสดงให้เห็นว่า เราสามารถเอาค่า (a, b) คืนจาก (x, y) ได้ด้วย แต่เฉพาะเมื่อ | u : v | ≠ 0 นะ

---

และแล้ว หัวเรื่อง Transformation ก็พร้อมที่จะเดินหน้าต่อแล้วครับ! โปรดติดตาม :D