Transformation Matrix: พื้นฐาน

หัวข้อ "ตามหาความหมายของ Determinant" ถึงว่าจบไปแล้ว แต่การเอา determinant มาใช้ยังไม่จบนะ ตอนนี้อยากให้คุ้นเคยกับ matrix ซะก่อน

คราวนี้จะแค่กำหนดสัญลักษณ์ต่าง ๆ สำหรับใช้ในตอนต่อ ๆ ไปนะ ไม่มีอะไรหวือหวา อ่านง่าย จบเร็ว...

อ้อ เกือบลืมบอกไป ... ตัวอย่างที่เอามาแสดงนี่เป็น 3 มิติ แต่จริง ๆ แล้วจะกี่มิติก็เหมือนกันนะ

เริ่มเลยละกัน ... สมมติว่า X Y A B C P Q R เป็น vector 3 มิติ

dot product (หรือ Inner Product) ของ vector สองตัว

X ตั้งฉากกับ Y ก็ต่อเมื่อ X ⋅ Y = 0 นะ

matrix ที่ได้จากการต่อ matrix ที่เล็กกว่า (คิดซะว่า vector ก็เป็น matrix)

การคูณ square matrix กับ vector

การคูณ square matrix 2 ตัว

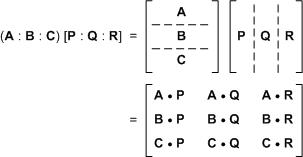
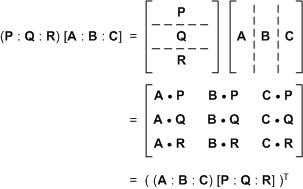
อันนี้ ถ้าลองมองให้
M = (A : B : C)
N = [P : Q : R]

จะเห็นว่า

(MN)^T = N^TM^T

จบแล้ว ... คราวหน้าจะมีเนื้อหาละ