Discrete vs Continuous: 1 + 4 + 9 + 16 + ... (ภาคสอง)

เดี๋ยวจะมีสัญลักษณ์ใหม่อีกตัวนึงนะ ขอเริ่มจากวิธีคิด slope ของฟังก์ชันก่อนนะ

จะเห็นว่า เมื่อให้ Δx → 0 เราจะได้สิ่งที่เรียกว่า อนุพันธ์ของ f(x) (เทียบกับ x)

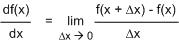
แล้วก็ให้ Δx → 1 หละ? สมการแรกก็จะกลายเป็น...

ตัวนี้แหละ ที่เราจะเอามาคิดกันต่อ

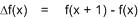
จากวิชาแคลคูลัส เรารู้ว่า

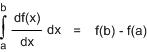
คราวนี้ลองหาผลบวกของ Δf(x) ดู (ถ้าใครจำ Σ ไม่ได้ ลองกลับไปดูตอนเก่า ๆ นะ)

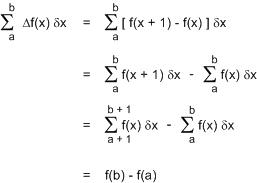
จะพอสังเกตเห็นได้ว่า...

1. แบบ Continuous: dy/dx → ผลต่าง, ∫y dx → ผลรวม
2. แบบ Discrete: Δy → ผลต่าง, Σy δx → ผลรวม

แล้ววิธีประยุกต์หละ? ลองกลับไปดูชื่อของหัวข้อนี้สิ :P เราจะหา 1² + 2² + 3² + ... + n² อีกรอบ แต่วิธีไม่เหมือนกันนะ

เริ่มจาก หาผลต่างของ f(x) = x³ ก่อน...

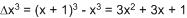
คราวนี้ ก็ใส่ Σ เข้าไปทั้งสองข้างเลย

ถูกแล้วหละ เพราะได้สูตรเดิมอีกแล้ว คือ

1² + 2² + 3² + ... + (n - 1)² = n(n - 1)(2n - 1)/6

ซึ่งมันแปลว่า

1² + 2² + 3² + ... + n² = n(n + 1)(2n + 1)/6

น่ะแหละ