ตามหาความหมายของ Determinant: Linear Combination
มาตามหาความหมายของ Matrix และ Determinant กันต่อนะ ขอทวนของเก่านิดนึง ...

ทำรูปให้ดูได้ถึงแค่ 3 มิติอะ พอถึง 4 มิติก็ไม่รู้จะวาดไง (ไม่รู้จะเรียกว่าอะไรด้วย) แต่แนวคิดก็ยังใช้ได้เหมือนกันนะ
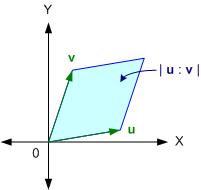
ผลรวมเชิงเส้น (Linear Combination) ของ u กับ v ในกรณี 2 มิติ ก็คือ vector ที่เขียนได้ในรูป
au + bv เมื่อ a, b ∈ R
จะเห็นว่า Linear Combination ของ u กับ v มีอยู่มากมายนับไม่ถ้วน (เพราะ R เป็นเซตที่นับไม่ได้)เซตของ Linear Combination ทั้งหมดของ u กับ v จะเขียนแทนด้วย
span(u, v) = { au + bv | a, b ∈ R }
รูปข้างล่างนี่ จะเห็นว่า u กับ v ทำให้เกิดระบบพิกัดใหม่ จากเดิมที่ใช้ x กับ y ก็กลายเป็น a กับ b

แต่มีกรณีนึง ที่ u กับ v ไม่ทำให้เกิดระบบพิกัดใหม่ ก็คือ เมื่อ u กับ v มีทิศทางเดียวกัน ซึ่งจะทำให้
| u : v | = 0
เราก็เลยสรุปได้ว่า
span(u, v) = R2 ก็ต่อเมื่อ | u : v | ≠ 0
จะ 3 มิติก็เหมือนกัน
span(u, v, w) = R3 ก็ต่อเมื่อ | u : v : w | ≠ 0
และไม่ว่าจะกี่มิติก็ตาม
span(u1, u2, u3, ..., un) = Rn ก็ต่อเมื่อ | u1 : u2 : u3 : ... : un | ≠ 0
เสริมนิดนึง
ถ้ากำหนด uspan (Unit Span) สำหรับกรณี 2 มิติให้เป็น
uspan(u, v) = { au + bv | a, b ∈ (0, 1) }
ก็จะเห็นว่า

พื้นที่ของ uspan(u, v) = | u : v |
กรณี 3 มิติ ก็เหมือนกัน คือ
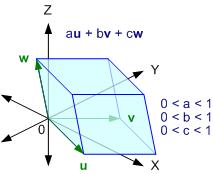
และ ... ในกรณี n มิติ (วาดรูปไม่ได้อีกแล้วอ่า)
จบจ้า ... แล้วตกลงรู้ความหมายของ det รึยังหละเนี่ย ... :P
ก็จะเห็นว่า

และ
uspan(u, v) ≠ ∅ ก็ต่อเมื่อ span(u, v) = R2กรณี 3 มิติ ก็เหมือนกัน คือ

ปริมาตรของ uspan(u, v, w) = | u : v : w |
uspan(u, v, w) ≠ ∅ ก็ต่อเมื่อ span(u, v, w) = R3
และ ... ในกรณี n มิติ (วาดรูปไม่ได้อีกแล้วอ่า)
ปริมาณ n มิติของ uspan(u1, u2, u3, ..., un) = | u1 : u2 : u3 : ... : un |
uspan(u1, u2, u3, ..., un) ≠ ∅ ก็ต่อเมื่อ span(u1, u2, u3, ..., un) = Rn
uspan(u1, u2, u3, ..., un) ≠ ∅ ก็ต่อเมื่อ span(u1, u2, u3, ..., un) = Rn
จบจ้า ... แล้วตกลงรู้ความหมายของ det รึยังหละเนี่ย ... :P
2 Comments:
ยังไม่ลง jsMath อีก!!?
ขี้เกียจหัดใช้อ่าพี่ ไว้ก่อน ไว้ก่อน (ผลัดวันประกันพรุ่งจริง ๆ เว้ย คนเรา 555)
Post a Comment
<< Home