สูตรเมื่อสมัยเด็ก - Hero's Formula

คราวนี้ ลองกลับมาขุดเรื่องสมัยเด็ก ๆ กันอีกทีดีกว่า (คราวนี้ต้องคิดตามเยอะหน่อยนะ เป็นเรื่องพีชคณิตล้วน ๆ เลย) เรื่องนี้เรียกว่า Hero's Formula หรือ Heron's Formula (มันมี 2 ชื่อ ... ได้ไงไม่รู้)

เข้าเรื่องเร็ว ๆ เลยละกัน สมมติว่ามีสามเหลี่ยมรูปนึง ที่เรารู้ความยาวด้านทั้งสาม

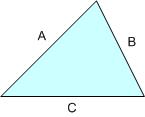
แล้วเราจะหาพื้นที่ของสามเหลี่ยมนี่ได้ยังไงหละ? ลากเส้นส่วนสูงแล้วกำหนดตัวแปรเพิ่มก่อนละกัน

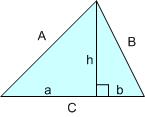
เอาหละ คราวนี้ลองมาดูว่าเราตั้งสมการอะไรได้บ้าง

(1)	A2 = h2 + a2
(2)	B2 = h2 + b2
(3)	C = a + b

เอาหละ มี 3 สมการ 3 ตัวแปรพอดีเลย มันต้องแก้ได้แหละนะ เริ่มโดยเอา (1) - (2) จะได้

A² - B² = a² - b²
A² - B² = (a - b)(a + b)

เนื่องจาก (3) แทนค่าลงไปจะได้

(4)	(A2 - B2)/C = a - b

คราวนี้ ตามสูตรมาตรฐานก็คือ (3) + (4) จะได้ 2a ออกมาแล้ว

C + (A² - B²)/C = 2a

เอา C คูณตลอด รูปจะได้สวย ๆ

2aC = A² - B² + C²

คราวนี้ ยกกำลังสอง เพื่อให้มันมี a² จะได้ใกล้เคียงกับสมการที่ (1)

(5)	4a2C2 = (A2 - B2 + C2)2

เอาสมการที่ (1) คูณด้วย 4C² รูปจะได้ตรงกันพอดีกับ (5)

4A²C² = 4h²C² + 4a²C²

เอา (5) มาแทนได้แล้วหละ

4A²C² = 4h²C² + (A² - B² + C²)²

ตอนนี้ติดตัวแปรเดียวคือ h ก็ย้ายข้างซะ

4h²C² = 4A²C² - (A² - B² + C²)²

4h²C² = (2AC + A² - B² + C²)(2AC - A² + B² - C²)

4h²C² = [(A + C)² - B²][B² - (A - C)²]

4h²C² = (A + C + B)(A + C - B)(B + A - C)(B - A + C)

4h²C² = (A + B + C)(-A + B + C)(A - B + C)(A + B - C)

เอาหละ ถอดรากเลย

2hC = sqrt[(A + B + C)(-A + B + C)(A - B + C)(A + B - C)]

เนื่องจากพื้นที่ของสามเหลี่ยมคือ hC/2 ดังนั้นคำตอบที่เราต้องการก็คือ

hC/2 = (1/4)sqrt[(A + B + C)(-A + B + C)(A - B + C)(A + B - C)]

ถ้าให้ s = (A + B + C)/2 จะได้ว่า

2s = A + B + C
2(s - A) = -A + B + C
2(s - B) = A - B + C
2(s - C) = A + B - C

ดังนั้น

พื้นที่ของสามเหลี่ยม = sqrt[s(s - A)(s - B)(s - C)]
s = (A + B + C)/2

จบแล้วจ้า นี่แหละที่เรียกว่า Hero's Formula หรือ Heron's Formula