ต่อจากสูตรเมื่อสมัยเด็ก - ปริมาตรของ Tetrahedron

ในเรื่อง ตามหาความหมายของ Determinant: Area & Volume กับเรื่อง สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนแรก) เราก็รู้มาแล้วว่า สูตรของพื้นที่ที่เกิดจากจุด 2 จุด (หรือ vector 2 เส้น) เป็นแบบนี้

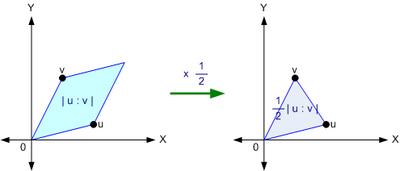
ลองมาขยายให้เป็นสามมิติซิ (ใช้แนวคิดแบบเดียวกับในเรื่อง ตามหาความหมายของ Determinant: Area & Volume)

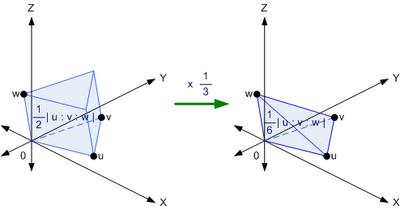
เอาหละ เรารู้แล้วว่าปริมาตรในรูปข้างบน (ขวา) นี้ เท่ากับ | u : v : w | / 6 คราวนี้ก็ใช้แนวคิดการรวมเข้าหักออกแบบที่เคยทำ (ในเรื่อง สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนจบ)) เราก็จะได้ว่า ปริมาตรของทรงเหลี่ยม 4 หน้าที่กำหนดด้วยจุดยอด 4 จุดเป็นดังนี้

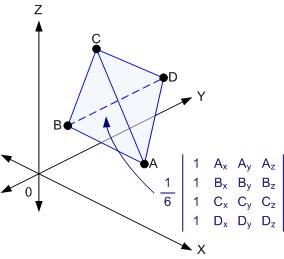
น่าเสียดายหน่อย ที่ปริมาตรของ Polyhedron ใด ๆ ไม่สามารถคำนวณได้ง่าย ๆ เหมือนกับพื้นที่ของ Polygon ใด ๆ ...

แต่เราก็พอเห็นไอเดียอะไรอีกอย่างนะ... ถ้าเรามีจุดใน 4 มิติอยู่ 5 จุด ปริมาณ 4 มิติของ space ที่มีจุดยอดเป็นจุดทั้ง 5 จุดที่กำหนดให้ ก็น่าจะมีค่าเท่ากับ

ซึ่งมันเป็นจริง ... แล้วก็ เมื่อขยายไปเป็น 5 มิติ หรือ 6 มิติ หรือจะกี่มิติก็ตาม หลักการนี้ก็ยังใช้ได้อยู่ (สังเกตด้วยว่าตัวหารของ n มิติก็คือ n! นะ)