พื้นที่ผิวของทรงกลม

คาดว่าทุกคนคงรู้กันอยู่แล้วว่าพื้นที่ผิวของทรงกลมที่มีรัศมี r เท่ากับ 4πr² ที่จะเอามาให้ดูตอนนี้ ไม่ใช่ (แค่) วิธีพิสูจน์หรอกนะ แต่เป็นอะไรที่น่าสนใจกว่านั้น

สมมติว่า เราอยากรู้พื้นที่บนผิวของทรงกลมตรงส่วนที่แรเงาของรูปนี้


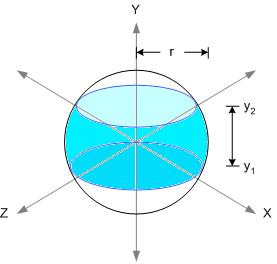
สมมติว่าพื้นที่ที่ต้องการหา มีค่าเท่ากับ A ลองคำนวณโดยใช้ Calculus ตรง ๆ ดูซิ


ตั้งสมการหา dA ดังนี้

dA = (2πr cos θ) ⋅ r dθ = 2πr² cos θ dθ

เปลี่ยนตัวแปรจาก θ เป็น y

y = r sin θ
dy = r cos θ dθ
แทนค่าคืนลงไปในสมการของ dA จะได้ ...

dA = 2πr dy
เอ๊ะ ทำไมมันง่ายแปลก ๆ ... ? ไหนลอง integrate ซิ

A = ∫dA = ∫2πr dy
A = 2πr∫dy
A = 2πry + C
พื้นที่ที่ต้องการหาในรูปแรก ก็เท่ากับ...

A(y₂) - A(y₁) = 2πr(y₂ - y₁)
เอ๊ะ ... นี่มันเท่ากับพื้นที่ผิวข้างของทรงกระบอกที่มีรัศมี r กับความสูง y₂ - y₁ พอดีเลยหนิ ... แปลกดีเนอะ ...

...

ไม่แปลกหรอ ......... T_T

ป.ล. : ให้ y₂ - y₁ = 2r ก็จะได้สูตร 4πr² นะ