สูตรสมัยเด็ก - สี่เหลี่ยมด้านขนาน (ปัจฉิมบท)

ดังที่กล่าวไว้ในตอนที่แล้ว เอาสี่เหลี่ยมอะไรก็ได้มาแบ่งครึ่งด้านทั้งสี่ ลากเส้นโยงที่จุดแบ่งเป็นรูปสี่เหลี่ยมอันใหม่ มันจะเป็นสี่เหลี่ยมด้านขนานแน่ ๆ

คราวนี้ จะมาแสดงวิธีพิสูจน์อย่างง่าย ๆ ให้ดูกันนะ มี 2 วิธี

วิธีแรก ใช้ความรู้แค่ม.ต้น แต่ต้องมองมากนิดนึง เริ่มต้นโดยการลากเส้นทแยงมุม

สังเกตรูปสามเหลี่ยมที่เกิดขึ้นให้ดี ๆ หละ ดูรูปข้างล่างนะ เส้นที่เป็นสีส้ม จะมีความยาวเป็นสองเท่าของเส้นสีน้ำเงิน และขนานกับเส้นสีน้ำเงิน

เห็นมั้ยว่ามันต้องเป็นสี่เหลี่ยมด้านขนานแน่ ๆ ... แต่ถ้าไม่แน่ใจ ลองตรวจดูอีกคู่นึงก็ได้

ชัวร์แล้วหละ มันเป็นสี่เหลี่ยมด้านขนานจริง ๆ!!!

เอาหละ คราวนี้ วิธีพิสูจน์อีกแบบ อันนี้ใช้ความรู้เรื่องเวกเตอร์ ดังนั้นต้องเป็นของม.ปลาย แต่ว่า ... วิธีมันไม่ใช้สมองเอาซะเลย ... โคตรตรง!

เอาหละ เริ่มโดยการ วางมุมล่างซ้ายของมันไว้ที่จุดกำเนิดของ Cartesian 2D space แล้วกำหนดเวกเตอร์ A B C ตามรูป

คราวนี้ จุดกึ่งกลางแต่ละด้านก็สามารถหาได้ง่าย ๆ โดยเอาจุดปลายทั้งสอง บวกกัน หารสอง...

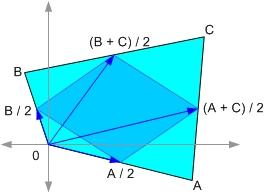
คราวนี้ ด้านของสี่เหลี่ยมอันใน ก็จะหาได้จากการเอาจุดปลายทั้งสองมาลบกัน...

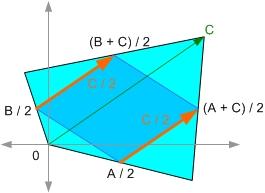
นี่ไง เวกเตอร์ทั้งสองอันเท่ากัน แปลว่ามันยาวเท่ากันแล้วก็ขนานกันด้วย ... อะ ลองให้แน่ใจอีกแนวซิ

เห็นมะ ... จบแล้ว