ตามหาความหมายของ Determinant: Area & Volume

คราวนี้ จะว่าเป็นภาคต่อของเรื่องพื้นที่ของ Polygon ก็อาจจะได้นะ แต่จริง ๆ ตอนนี้มีจุดประสงค์คืออยากให้เห็นประโยชน์อีกอย่างนึงของ det มากกว่า แต่ตอนหลัง ๆ จะมีอะไรต่อไปอีกแน่นอน

เอาหละ จากตอนแรกเลย เรารู้ว่า...

ซึ่งถ้าเราต่ออีกด้านไปให้พื้นที่เพิ่มเป็นสองเท่าของเดิม จะได้รูปนี้...

คราวนี้ ลองมองเป็นเวกเตอร์ดูบ้าง เอาหละ...

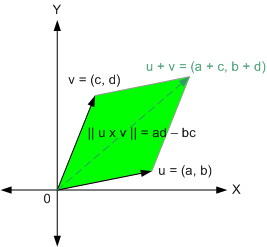
นี่หละที่อยากจะเอาให้ดู

คราวนี้ลองมองเป็นสามมิติดูบ้าง (คาดว่าบางคนอาจจะเริ่มรู้สึกคุ้น ๆ)

ปริมาตรของรูปข้างบนนี่ น่าจะหาได้ด้วยวิธีคล้าย ๆ กันนะ (ตอนนี้บางคนคงจะคุ้น ๆ แล้ว ... ไม่นับคนที่รู้อยู่แล้วนะ)

ลองหาพื้นที่แผ่น ๆ ในแนว u กับ v ก่อน ใช้สูตรเมื่อกี๊อะนะ

แต่ u x v มันมีทิศนี่นา ตั้งฉากกับไอ้แผ่นเมื่อกี๊แหละ (ไม่ต้องไปสนใจความยาวของมันในรูปนี้นะ)

คราวนี้ ถ้าก็เอาพื้นที่คูณกับความยาวในแนวตั้งฉาก ก็จะได้ปริมาตรแน่นอน แต่จะคูณยังไงหละ?

ใช้ Dot Product ไง... ได้แล้ว

นี่หละ ปริมาตรของก้อนที่ต้องการ ... แล้วถ้าคิดในเทอมของ a b c d e f g h i หละ?

คิดยาก ... เหรอ? บอกให้เลยละกันจะได้ไม่ต้องไปทด

นี่หละ ความไม่น่าเชื่อ!!! ผลคูณนี่เค้าก็มีชื่อเรียกกันว่า Scalar Triple Product (อยู่ในวิชา Calculus 2 มั้ง)

แล้วใน 4 มิติหละ ถ้ามีเวกเตอร์ 4 มิติ 4 เส้น เราจะหาค่า XXX (ไม่รู้จะเรียกว่าไรอะ) ได้ด้วยวิธีเดียวกันรึเปล่าน้า...

จบตอนละ ตอนหน้าจะบอกวิธีประยุกต์สูตรนี้ให้ ... แต่ไม่ใช่เรื่องมิติที่ 4 นะ