Transformation Matrix: The Rotation Matrix in 2D

ก็เนื่องจาก เราเห็นว่าเรื่องนี้มันง่ายดี และมีความสัมพันธ์กับสิ่งลึกลับอย่าง matrix ด้วย ก็เลยหยิบมาให้ดู คาดว่าหลายคนคงรู้แล้วหละ แต่คนที่ไม่รู้คงได้ประโยชน์บ้างอะนะ ขอโทษด้วยที่ใช้สมการเยอะหน่อย

โจทย์ก็มีอยู่ว่า ถ้ามีจุด (x, y) อยู่ แล้วต้องการหมุนไปเป็นมุม θ ทวนเข็มนาฬิกา (ถ้าต้องการให้หมุนตามเข็มก็ให้ค่า θ น้อยกว่า 0) พอหมุนเสร็จแล้วเนี่ย จุดมันจะไปอยู่ที่ไหน? ... สมมติให้เป็น (x', y') ละกัน

เพื่อให้ง่ายต่อการหาค่า (x', y') เราก็จะกำหนดค่ามุมเพิ่มขึ้นมาค่าหนึ่ง คือ α (สังเกตในรูปดี ๆ นะ มันตัวเล็ก)

เอาหละ เราได้สมการที่จะใช้เริ่มต้นแล้ว

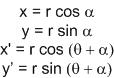
ความซับซ้อนจะมีแค่ตรงนี้แหละ จากสูตรตรีโกณสองสูตรนี้

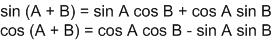
เมื่อแทนค่าลงไป จะได้...

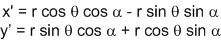
แทนค่าด้วยสมการเริ่มต้นเพื่อให้ α หายไปโดย...

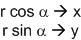
ก็จะได้

ซึ่งเขียนเป็นสมการของ matrix ได้แบบนี้

ตัว square matrix ที่คูณอยู่ข้างหน้า [x, y]^t นี่แหละ ที่เราเรียกว่า "Rotation Matrix" หรือ เมตริกซ์การหมุน

ความพิเศษของเมตริกซ์การหมุนก็คือ สามารถหา inverse ได้ง่ายเหลือเกิน...

จริง ๆ จะลองใช้สูตรของ matrix ในการหา inverse matrix ก็ได้ ผลลัพธ์จะเหมือนกัน

เห็นอะไรมั้ยอย่างนึง... det(R(θ)) = 1 ซึ่งก็แปลว่า พี้นที่ของสี่เหลี่ยม (บังเอิญว่าขนมเปียกปูน) ที่มีจุดยอดอยู่ที่

1. (0, 0)
2. (cos θ, -sin θ)
3. (cos θ + sin θ, cos θ - sin θ)
4. (sin θ, cos θ)

เท่ากับ 1

จะสังเกตไปทำไม............ไม่รู้เหมือนกัน!!!