Discrete vs Continuous: 1 + 4 + 9 + 16 + ... (ภาคแรก)

คราวที่แล้ว เราใช้วิธีมองกราฟเพื่อพิสูจน์ว่า

1 + 2 + 3 + ... + n = n(n + 1)/2

คราวนี้เราจะใช้วิธีเดียวกันอีกทีนึง เพื่อพิสูจน์ว่า

1² + 2² + 3² + ... + n² = n(n + 1)(2n + 1)/6

ไม่พูดมากละกัน ดูรูปเอา

จะเห็นว่า ในแต่ละช่อง จะมีผลต่างของอินทิกรัลกับผลบวกอยู่ สมการของค่าที่เราต้องการก็จะเป็น

summation = integral - error

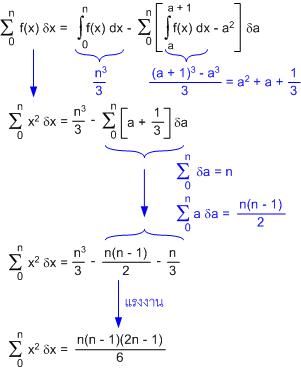
นี่หละ ตัวอย่างการประยุกต์ใช้แนวคิด "มองจากกราฟ"

ถ้าไปทดลองต่อ จะเห็นว่าเราสามารถขยายสูตรของผลบวกของ x^d เมื่อ x ∈ {1, 2, ..., n } ได้เรื่อย ๆ ด้วยวิธีการมองจากกราฟ ไม่ว่า d จะเป็นเท่าไหร่ก็ตาม (แต่ต้องเป็นจำนวนเต็มบวกนะ)

คราวหน้าจะพูดถึง "ผลต่าง" บ้างละ ... แล้วเราก็จะพิสูจน์สูตรนี้ได้ด้วยอีกวิธีนึง ซึ่งเร็วกว่าวิธีนี้ แต่ต้องใช้ความรู้มากกว่านิดหน่อยนะ