Center of Mass & Centroid - Polygon

คราวนี้ จะขยายเรื่องของค่าเฉลี่ยถ่วงน้ำหนักก่อน นิดนึง

เนื่องจาก ผลคูณภายใน มันก็ไม่ได้ห้ามตัวเลขตัวไหนติดลบ ทำไมเราจะใช้ "น้ำหนักติดลบ" ไม่ได้เนอะ

แล้วมันเกี่ยวอะไรกับการหาจุดศูนย์กลางมวลกับ centroid หละ?

เอาตัวอย่างเลยละกัน สมมติเราจะหา centroid ของรูปนี้

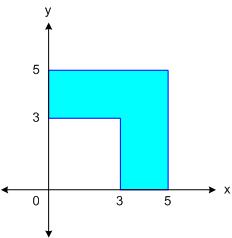
เราจะใช้วิธีหาค่าเฉลี่ยถ่วงน้ำหนักได้ง่าย ๆ หยั่งงี้

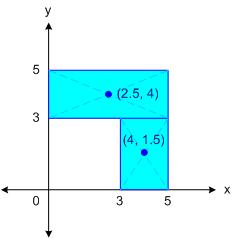
คำตอบก็คือ

(10 ⋅ (2.5, 4) + 6 ⋅ (4, 1.5)) / (10 + 6) = (25 + 24, 40 + 9) / 16
= (49/16, 49/16)

แต่เราอาจจะใช้อีกวิธีนึง (ทาง Combinatorics เรียกว่า "หลักการการรวมเข้าหักออก" หรือ "Inclusion-Exclusion Principle") ก็คือ น้ำหนักติดลบ แบบนี้

กับ

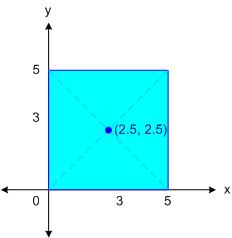
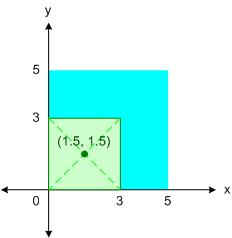
คำตอบก็คือ

(25 ⋅ (2.5, 2.5) - 9 ⋅ (1.5, 1.5)) / (25 - 9) = (62.5 - 13.5, 62.5 - 13.5) / 16
= (49/16, 49/16)

แล้วหลักการนี้มันใช้ประโยชน์อะไรได้อีก ... ดูชื่อหัวข้อสิ :P

คงต้องบอกอะไรอย่างหนึ่งก่อนนะ คือ ... centroid ของรูปสามเหลี่ยมใด ๆ ก็คือ centroid ของจุดยอดทั้ง 3 ของสามเหลี่ยมนั้น ... ไม่งงนะ ?

คราวนี้ สมมติว่า เราจะหา centroid ของรูปนี้ ซึ่งเรารู้พิกัดของจุดยอดหมดแล้ว (จำรูปนี้ได้ป่าวเอ่ย)

เราก็หา centroid แต่ละชิ้น ถ่วงน้ำหนักด้วยพื้นที่ของมัน (ลองไปดู สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนที่สอง) กับ สูตรเมื่อสมัยเด็ก - พื้นที่ของ Polygon (ตอนจบ) นะ ถ้าจำไม่ได้)

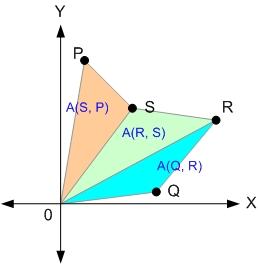
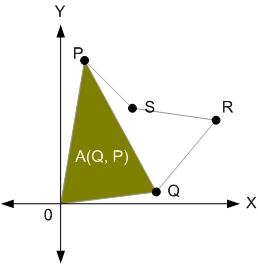
หาค่าเฉลี่ยถ่วงน้ำหนัก ก็จะได้ centroid ของรูปที่ต้องการ

สำหรับรูปตัวอย่างนี้ (จริง ๆ คือ รูป 4 เหลี่ยมใด ๆ) ถ้าคิด P Q R S เป็น vector เราจะหา centroid ได้ง่าย ๆ จากสมการต่อไปนี้ (ถ้าจำสัญลักษณ์ | P : Q | ไม่ได้ ลองไปดู ตามหาความหมายของ Determinant: เวกเตอร์ตั้งฉาก นะ)

a = | P : Q |
b = | Q : R |
c = | R : S |
d = | S : P |
C = [a(P + Q) + b(Q + R) + c(R + S) + d(S + P)]
÷ [3(a + b + c + d)]

ข้อสังเกต: พื้นที่ของสามเหลี่ยม คือ | P : Q | / 2 แต่เราเอา / 2 ออกไปได้ เพราะมันจะตัดกันเอง ส่วน centroid ของสามเหลี่ยม คือ (P + Q) / 3

หลักการนี้ จะขยายเป็น polygon กี่จุด มันก็เหมือนกันหนะนะ