ตรรกศาสตร์: ต้นไม้การพิสูจน์ และต้นไม้ตัวอย่างขัดแย้ง

เดี๋ยวจะแสดง algorithm สำหรับพิสูจน์ว่า "ประพจน์เป็นสัจพจน์หรือไม่" ให้ดู

สมมติว่าเรามีประพจน์

(A ∧ B ∧ C) → (D ∨ E ∨ F)

เพื่อให้เขียนสะดวก เราจะใช้สัญลักษณ์นี้แทน

A, B, C → D, E, F

ประพจน์นี้ จะเป็นเท็จก็ต่อเมื่อ ทุกตัวทางซ้ายเป็นจริง และทุกตัวทางขวาเป็นเท็จ

คราวนี้ ถ้ามีประพจน์ตัวนึงที่อยู่ทั้งสองฝั่ง เช่น

A, B → A, C

เราจะสรุปได้ทันทีว่าประพจน์นี้เป็นจริง

Algorithm - Constructing Trees

วิธีตรวจสอบความเป็นสัจพจน์ที่จะพูดถึง ก็คือ การพยายามหาเงื่อนไขที่ทำให้ประพจน์ไม่เป็นจริง ถ้าเราหาไม่ได้ แสดงว่ามันเป็นสัจพจน์

หลักการก็คือ พยายามทำให้ทุกตัวทางขวาเป็นเท็จ และพยายามทำให้ทุกตัวทางซ้ายเป็นจริง เอาตัวอย่างไปดูดีกว่า น่าจะเข้าใจง่ายกว่า ... สมมติว่าโจทย์คือ

ฝั่งซ้ายเราก็กระจายเครื่องหมาย "∨" เข้าไป ส่วนฝั่งขวา ก็แปลง "∨" ให้เป็น ","

(โดยทั่วไปเค้าจะเขียนจากล่างขึ้นบนกันนะ)

คราวนี้ เราต้องการทำให้เทอม "P ∨ Q" ที่อยู่ฝั่งซ้ายเป็นจริง ก็แยกได้สองกรณี คือ P เป็นจริง หรือ Q เป็นจริง ดังนี้

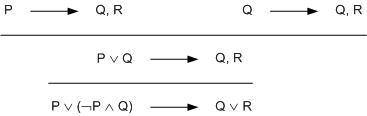
ประพจน์ที่เกิดขึ้นทางซ้าย ไม่มีพจน์หน้าตาซ้ำกัน กรณีนี้เราเรียกว่าเกิด ตัวอย่างขัดแย้ง (Counterexample) ซึ่งก็แปลว่า ถ้าให้ P เป็นจริง และ Q กับ R เป็นเท็จ ประพจน์นี้จะไม่เป็นจริง

แล้วก็ ... เราลองอ่านย้อนลงมาจากข้างบน เราก็จะเห็นขั้นตอนการแสดง ว่าทำไมประพจน์ตั้งต้น
(ที่อยู่ล่างสุด) มันถึงไม่เป็นสัจพจน์

รูปที่เราสร้างขึ้นมานี่ เรียกว่า "ต้นไม้ตัวอย่างขัดแย้ง" (Counterexample Tree)

คราวนี้ลองดูกรณีที่มันเป็นสัจพจน์บ้าง สมมติว่าโจทย์คือ

เราก็ค่อย ๆ แปลงให้อยู่ในรูปของเครื่องหมาย "," ก่อน แล้วทำให้มันดูง่ายที่สุด

(อย่าลืมว่า ล่างขึ้นบน)

คราวนี้ เราก็เลือกพจน์ทางซ้ายที่ยังมีตัวเชื่อม "∨" อยู่ แล้วแตกออกเป็นสองกรณี เหมือนในตัวอย่างที่แล้ว

(ขอตัดส่วนข้างล่างทิ้งนะ จะได้ไม่รก)

ประพจน์ใหม่ฝั่งซ้าย มี P อยู่ทั้งหัวและท้ายลูกศร จึงเป็นสัจพจน์ คราวนี้ลองดูประพจน์ใหม่ฝั่งขวาบ้าง จะเห็นว่ายังแตกต่อได้อีก

คราวนี้ ประพจน์ใหม่ที่เกิดขึ้น เป็นสัจพจน์ทั้งหมด ก็เลยไม่ต้องแตกต่อแล้ว สรุปได้เลยว่าประพจน์ตั้งต้นเป็นสัจพจน์

รูปที่สร้างอันนี้ เรียกว่า "ต้นไม้การพิสูจน์" (Proof Tree)

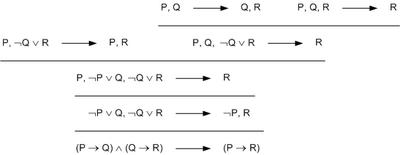
จะเห็นว่า ถ้าอ่านจากบนลงล่าง ก็จะได้วิธีพิสูจน์ความเป็นสัจพจน์ ของประพจน์ตั้งต้น (ตรงที่มีการแตก การรวม ถ้าอ่านลง ให้คิดว่าเป็นคำว่า "และ")

สรุป

ทุก ๆ ครั้งที่เราแตกต่อ จำนวนเครื่องหมายมันจะลดลงเรื่อย ๆ ถ้าเครื่องหมายหมดแล้ว มันก็มีอยู่ 2 กรณี คือ
1. เกิดตัวอย่างขัดแย้ง หรือเป็นสัจพจน์ ซึ่งถ้าเราเจอตัวอย่างขัดแย้งครั้งนึง ก็ให้หยุดได้เลย มันไม่เป็นสัจพจน์แน่นอน
2. เจอสัจพจน์ เราก็ต้องลองคิดกรณีอื่น ๆ ที่แตกไว้ต่อไป

แล้วถ้า?

ถ้าประพจน์ที่ต้องการพิสูจน์ ไม่ได้อยู่ในรูปแบบ "ถ้า...แล้ว" (A → B) หละ?

ก็เอาไว้ฝั่งขวาแต่เริ่มเลยสิ เพราะวิธีพิสูจน์ก็คือ เราจะหาวิธีทำให้มันเป็นเท็จไงหละ (จำได้มั้ยว่า อยู่ฝั่งขวา แปลว่า เราจะพยายามทำให้เป็นเท็จ)

อีกมุมมองนึง (แต่จริง ๆ แล้วเหมือนกัน) ก็คือ

→ P

แปลว่า ไม่ต้องรู้อะไรเลย ก็สรุปได้ว่า P หรือก็คือ P เป็นจริงเสมอ น่ะแหละ