Discrete vs Continuous: เทคนิคการหาผลบวก

เดี๋ยวจะลุยเทคนิคการหาผลบวกละ ขอทวนของเก่าก่อน สัญลักษณ์ที่จะใช้สำหรับผลบวก เป็นหยั่งงี้นะ

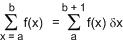
ดูดี ๆ หละ index ไม่เหมือนกัน ... แล้วก็ สัญลักษณ์ของผลต่าง

Δ f(x) = f(x + 1) - f(x)

คราวที่แล้ว เรารู้จักผลต่างและผลบวกของฟังก์ชัน พหุนามแบบมีขีดล่าง (ไม่รู้จะเรียกว่าไรดีอะ) xⁿ ไปแล้ว

xn	=	x(x - 1)(x - 2)...(x - n + 1)
Δ(xn)	=	nxn - 1
Σ xn δx	=	xn + 1/(n + 1) + c

ซึ่งหน้าตามัน ละม้ายคล้ายกับ

d(xn)/dx	=	nxn - 1
∫ xn dx	=	xn + 1/(n + 1) + c

ลองมาหาฟังก์ชันอื่น ๆ บ้าง

Δ(2x)	=	2x + 1 - 2x
Δ(2x)	=	2x

โอ๊ะ! มันคล้าย ๆ กับ e^x ในแคลคูลัสเลยหนิ เพราะว่า d(e^x)/dx = e^x

แล้วถ้าเปลี่ยนฐานหละ?

Δ(a^x) = a^{x + 1} - a^x
Δ(a^x) = (a - 1) a^x

ก็คล้าย ๆ กับในแคลคูลัสนะ แต่ค่าคงที่มาคูณข้างหน้ามันต่างกัน (ให้ดูเผื่อขี้เกียจคิด: d(a^x)/dx = (ln a) a^x)

คราวนี้ก็ได้สูตรของผลบวกอีกสูตรละ

Σ a^x δx = a^x/(a - 1) + c

คราวนี้มาลองหาอะไรที่มันใกล้ ๆ กับ ln แบบ discrete ดีกว่า เริ่มจาก ...

∫ (1/x) dx = ln x + c

ลองเปลี่ยนฝั่งซ้ายเป็น Σ ดูสิ

Σ (1/x) δx = (1 + 1/2 + 1/3 + ... + 1/(x - 1)) + c เมื่อ x > 0

อนุกรม 1 + 1/2 + 1/3 + ... + 1/(x - 1) เรียกว่า อนุกรมฮาร์โมนิก (Harmonic Series) เราจะใช้สัญลักษณ์ har x เพื่อแทนอนุกรมนี้นะ สูตรนี้ก็จะเขียนใหม่ได้เป็น

Σ (1/x) δx = har x + c

ผลต่างของ har x ก็คือ

Δ(har x) = 1/x

ข้อสังเกต: โดเมนของ ln x คือ (0, ∞) และโดเมนของ har x คือ {1, 2, 3, ...}

แล้วเอาไปใช้ยังไงหละ? ลุยต่อนะ ต่อไปนี้จะแสดงถึง Summation By Parts

ดูสัญลักษณ์ใหม่ก่อน ตัวนี้แปลว่า "ค่าถัดไป"

E f(x) = f(x + 1)

คุณสมบัติสำคัญของ E ก็คือ

E[f(x) + g(x)] = E[f(x)] + E[g(x)]
E[f(x) g(x)] = E[f(x)] E[g(x)]
E[f(g(x))] = f(E[g(x)])

ความสัมพันธ์ของ Δ กับ E ก็คือ

Δ = E - 1

ต่อไปนี้คือ ผลต่างของผลคูณ สมมติว่า u กับ v เป็นฟังก์ชันของ x นะ

Δ[uv]	=	(E - 1)[uv]
	=	E[uv] - uv
	=	E[u]E[v] - uv

ลองเอา uE[v] บวกเข้าแล้วลบออก

Δ[uv]	=	E[u]E[v] - uE[v] + uE[v] - uv
	=	(E[u] - u)E[v] + u(E[v] - v)
	=	(E - 1)[u]E[v] + u(E - 1)v
	=	u Δv + Ev Δu

ได้สูตรแล้ว หน้าตาคล้าย ๆ กับ d(uv) = u dv + v du เนอะ

เมื่อกี๊เราเอา uE[v] บวกเข้าแล้วลบออก แต่จริง ๆ แล้วเราเอา vE[u] แทนก็ได้ สูตรจะเป็น

Δ[uv] = Eu Δv + v Δu

คราวนี้ เราหาผลรวมสองข้าง (ใช้สูตรบนนะ เพราะอยากได้สูตรของ Σ u Δv δx)

uv = Σ u Δv δx + Σ Ev Δu δx

ย้ายข้าง ก็จะได้สูตร by parts

Σ u Δv δx = uv - Σ Ev Δu δx

เอามาใช้ยังไงหละ? ลองดูโจทย์ integration by parts ง่าย ๆ ก่อนอันนึงละกัน

∫ xex dx	=	∫ x [d(ex)/dx] dx
	=	xex - ∫ ex [d(x)/dx] dx
	=	xex - ex + c

คราวนี้ลองคิดเหมือนกัน แต่เป็นแบบผลบวก

Σ x2x δx	=	Σ x [Δ(2x)] δx
	=	x2x - Σ 2x + 1 [Δ(x)] δx
	=	x2x - 2 ⋅ 2x + c

คิดได้เกือบเหมือนกันเลย ต่างกันนิดนึงก็เพราะว่าสูตร summation by parts มันมีตัว E ห้อยอยู่หน้า v น่ะเอง คราวนี้พอก่อนนะ เดี๋ยวมาเล่นกับพวกนี้อีก